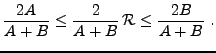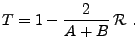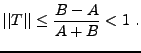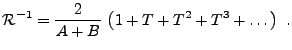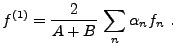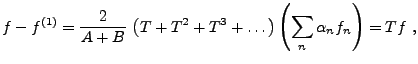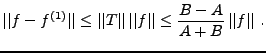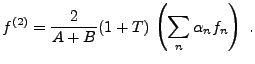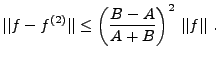Sous-sections
Repères dans un espace de Hilbert
Il existe des situations dans lesquelles on a intérêt,
plutôt que d'utiliser des bases orthonormées, à utiliser des familles
de fonctions qui sont complètes mais pas libres. On parle alors de familles
surcomplètes, ou de repères. La famille sur laquelle l'on décompose
le signal n'étant pas libre, les coefficients de la décomposition sont
redondants, et la représentation n'est donc pas ``économique''.
Cependant, on verra que cette représentation présente l'avantage d'être
plus robuste, c'est à dire moins sensible aux perturbations, qu'une
décomposition par rapport à une base.

EXEMPLE B..1 Considérons le plan
, muni d'une base orthonormée
.
Alors,
en posant
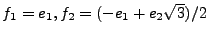
et
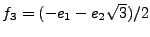
,
il est immédiat que
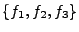
est un repère strict de
:
pour tout

, on a
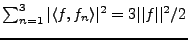
.
Plus généralement, toute famille finie de vecteurs est un repère de
l'espace qu'elle engendre.
On associe naturellement à un repère les deux opérateurs suivants:
l'opérateur
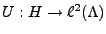 , défini par
, défini par
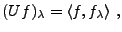 |
(B.1) |
et
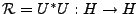 , défini par
, défini par
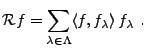 |
(B.2) |
Le résultat suivant est vérifié sans difficulté.

Preuve:
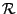 est auto adjoint: en effet, pour tous
est auto adjoint: en effet, pour tous 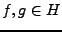 , on a
, on a
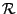 est borné: Calculons, pour
est borné: Calculons, pour 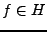
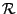 est injectif: soit
est injectif: soit  tel que
tel que
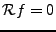 .
Alors
.
Alors
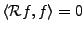 ,
et donc
,
et donc 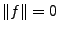 , qui implique
, qui implique 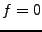 .
.
 est surjectif: pour tout
est surjectif: pour tout 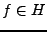 , on a
, on a
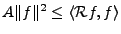 .
.
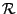 est borné inférieurement,
donc surjectif.
est borné inférieurement,
donc surjectif.
Par conséquent,
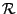 est bijectif. Comme on a de plus
pour tout
est bijectif. Comme on a de plus
pour tout 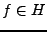 ,
,
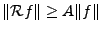 , on en déduit que
, on en déduit que
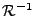 est borné également.
est borné également.

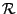 étant auto adjoint, il résulte de (
étant auto adjoint, il résulte de (![[*]](crossref.png) )
que son spectre est inclus dans l'intervalle
)
que son spectre est inclus dans l'intervalle ![$ [A,B]$](img1362.png) , ce
que l'on écrit aussi
, ce
que l'on écrit aussi
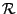 étant inversible, on peut écrire, pour tout
étant inversible, on peut écrire, pour tout
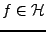
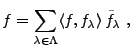 |
(B.3) |
oú on a posé
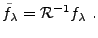 |
(B.4) |
Les
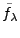 possèdent des propriétés
similaires à celles des
possèdent des propriétés
similaires à celles des 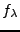 . En particulier:
. En particulier:
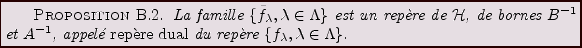
Preuve: La proposition résulte de l'estimation
suivante, qui est facilement vérifiée: pour tout 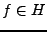 ,
,
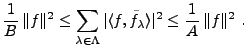 |
(B.5) |

On a donc aussi l'égalité, pour tout
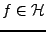
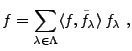 |
(B.6) |
REMARQUE B..1 Dans le cas d'un repère strict, c'est à dire dans le cas
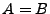
,
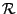
est un multiple de l'identité, de sorte que l'on a pour tout
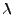
,
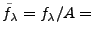
. On a ainsi, pour
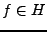
,
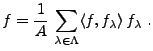 |
(B.7) |
Dans le cas général, il est nécessaire d'utiliser la
formule (
![[*]](crossref.png)
) pour expliciter un
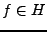
à partir
des coefficients
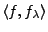
, ce qui n'est pas toujours
facile car
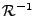
ne possède pas de forme explicite en général.
On verra un peu plus loin comment résoudre ce problème.
EXEMPLE B..2 Des exemples utiles de repères sont donnés par les repères
trigonométriques.
On sait que le système trigonométrique, formé des fonctions
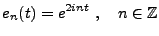 |
(B.8) |
est une base de
![$ L^2([0,\pi])$](img1285.png)
. Considérons le système de fonctions
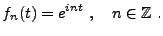 |
(B.9) |
Soit
![$ f\in L^2([0,\pi])$](img1380.png)
. Alors
où
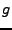
est définie par
L'égalité de Parseval donne alors
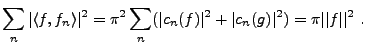 |
(B.10) |
Donc, la famille
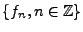
est un repère strict de
![$ L^2([0,\pi])$](img1285.png)
,
de borne
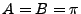
.
De tels repères, ou plutôt leurs analogues
finis, sont utilisés par exemple en restauration d'images, c'est
à dire pour reconstituer des images dont certains pixels sont
manquants.
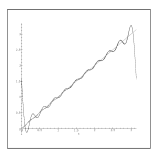
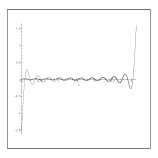
Figure:
Comparaison d'une série de Fourier usuelle et d'une
décomposition redondante: le cas d'une fonction linéaire.
A gauche, la fonction, sa reconstruction à partir de 11
modes de Fourier 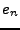 et 21 fonctions
et 21 fonctions 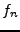 ; au centre, même
chose, avec 21 fonctions
; au centre, même
chose, avec 21 fonctions 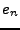 et 41 fonctions
et 41 fonctions 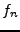 ; à
droite, les erreurs de reconstruction.
; à
droite, les erreurs de reconstruction.
|
|
Considérons maintenant l'opérateur 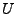 défini en (
défini en (![[*]](crossref.png) ).
Il est possible de donner une caractérisation de l'image de
).
Il est possible de donner une caractérisation de l'image de  par
par 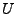 .
Dans le cas d'une base orthonormée
.
Dans le cas d'une base orthonormée
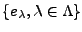 de
de
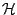 , le théorème de Riesz-Fisher établit une
correspondance bijective entre
, le théorème de Riesz-Fisher établit une
correspondance bijective entre
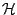 et
et
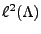 . Dans le
cas d'un repère, la suite
. Dans le
cas d'un repère, la suite 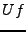 des coefficients
des coefficients
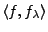 de
de
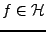 est bien dans
est bien dans
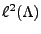 . Il résulte de la définition que
. Il résulte de la définition que 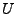 est injectif,
et que
est injectif,
et que
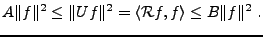 |
(B.11) |
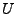 n'est pas nécessairement surjectif. En fait, si les éléments du
repère
n'est pas nécessairement surjectif. En fait, si les éléments du
repère
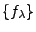 sont linéairement dépendants,
sont linéairement dépendants, 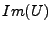 est
strictement inclus dans
est
strictement inclus dans
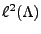 . En effet supposons que la suite
. En effet supposons que la suite
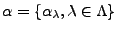 soit telle que
soit telle que
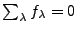 . Alors on peut écrire, pour
. Alors on peut écrire, pour 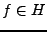 :
:
de sorte que
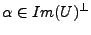 .
. 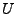 étant injectif, il possède
un inverse défini sur
étant injectif, il possède
un inverse défini sur 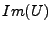 , que l'on peut prolonger de façon
arbitraire à
, que l'on peut prolonger de façon
arbitraire à
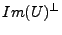 .
.
Parmi tous les inverses à gauche possibles, on utilise généralement
le pseudo-inverse
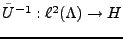 , défini par
, défini par
![$\displaystyle \tilde U{^{-1}}\left[ Im(U)^\perp\right]=0\ .$](img1398.png) |
(B.12) |
Le résultat suivant donne une description plus ``géométrique''
de la situation.

Preuve:
Soit
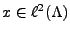 . Il admet une unique décomposition
. Il admet une unique décomposition
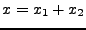 , avec
, avec
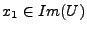 et
et
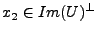 . On suppose
. On suppose
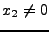 . Soit
. Soit 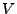 un inverse à gauche de
un inverse à gauche de 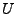 . Alors on a
. Alors on a
Donc,
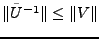 .
.
Soit
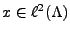 . Alors, il existe
. Alors, il existe 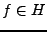 tel que
tel que 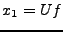 .
On a alors, en utilisant (
.
On a alors, en utilisant (![[*]](crossref.png) ),
),
Calculons enfin
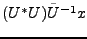 ,
pour
,
pour
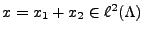 . Il est clair que
. Il est clair que
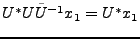 . On a aussi par définition
. On a aussi par définition
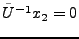 . Reste à montrer que
. Reste à montrer que 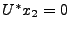 . Soit
. Soit
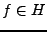 . On a
. On a
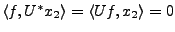 .
On a donc bien
.
On a donc bien
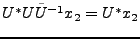 , ce qui achève la preuve.
, ce qui achève la preuve.

L'opérateur
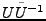 possède un statut particulier,
comme le montre le corollaire suivant:
possède un statut particulier,
comme le montre le corollaire suivant:

Preuve:
Avec les mêmes notations que ci dessus, soit
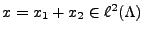 (où
(où
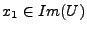 ). On a
). On a 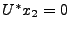 , et il existe
, et il existe 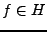 tel que
tel que
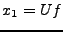 , et
, et
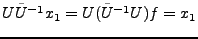 . Donc
il s'agit bien d'un projecteur orthogonal.
. Donc
il s'agit bien d'un projecteur orthogonal.
Par définition, on a
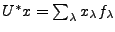 . Donc,
. Donc,
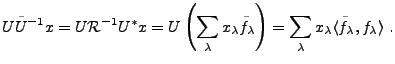

REMARQUE B..2
Utilité des décompositions redondantes: Les décompositions redondantes apportent une stabilité
supplémentaire aux décompositions. En effet, soit
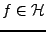
un vecteur
fixé, et soit
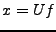
. Supposons qu'une erreur
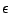
soit commise sur
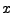
: soient
En notant
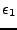
la projection de
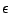
sur
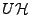
, et
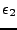
sa projection sur
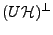
, on voit immédiatement
que
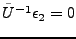
, et que donc
Ainsi, la composante
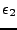
de l'erreur disparait lors de
l'inversion de la décomposition. On voit donc que dans des
situations où on se doute à l'avance qu'une erreur importante
va être commise sur les coefficients, lors d'une étape de
transmission par exemple, on a intérêt à utiliser des
décompositions par rapport à des repères de préférence à des
décompositions sur des bases, car une partie de l'erreur disparaitra
lors de la resynthèse.
REMARQUE B..3 Dans un contexte de traitement du signal, des décompositions
redondantes telles que des décompositions par rapport à des repères
trouvent leur utilité pour le codage des signaux, dès que l'on
s'attend à ce que le signal codé soit perturbé par un ``bruit''.
La question qui se pose en pratique est la suivante: étant donnés
les coefficients de 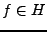 par rapport à un repère
par rapport à un repère
 , comment retrouver
, comment retrouver  à partir de ces
coefficients ?
à partir de ces
coefficients ?
Nous connaissons déjà la réponse dans le cas d'un repère
strict, puisque dans ce cas l'opérateur
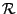 est un multiple
de l'identité. La situation est un peu plus complexe dans le cas
général, puisqu'il faut utiliser la relation
est un multiple
de l'identité. La situation est un peu plus complexe dans le cas
général, puisqu'il faut utiliser la relation
et
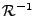 n'est pas connu explicitement.
n'est pas connu explicitement.
Considérons l'opérateur de repère
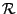 . On sait que
. On sait que
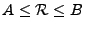 . Par conséquent, on a aussi
. Par conséquent, on a aussi
Posons
Un calcul immédiat montre que
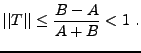 |
(B.13) |
Par conséquent, l'opérateur 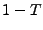 est inversible, et la série de
Neumann correspondante
est inversible, et la série de
Neumann correspondante
est convergente. On peut donc écrire
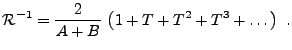 |
(B.14) |
Ceci conduit à l'algorithme d'inversion suivant: en posant
on commence par évaluer
On sait alors que
de sorte que
Si la précision est suffisante, c'est à dire si la constante
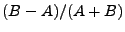 est assez faible, on se contentera de
est assez faible, on se contentera de  comme approximation de
comme approximation de  . Si tel n'est pas le cas, il faut
pousser plus loin le développement, et considérer
. Si tel n'est pas le cas, il faut
pousser plus loin le développement, et considérer
On a alors évidemment un ordre d'approximation supplémentaire:
REMARQUE B..4 L'algorithme d'inversion qu'on a vu ci-dessus a l'avantage d'être
simple, mais n'est pas optimal. En pratique, il est souvent plus
avantageux d'utiliser des méthodes classiques d'inversion, telles
que des méthodes de gradient conjugué par exemple.
REMARQUE B..5 Il est possible de montrer que les bases orthonormées que nous avons
vues plus haut peuvent être remplacées par des repères construits
de la même manière. C'est en particulier le cas des
bases trigonométriques locales (on construit facilement des repères
trigonométriques locaux), et des ondelettes, pour lesquelles il est même
plus facile de construire des repères ue des bases.
Bruno Torresani
2007-06-26

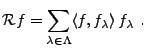
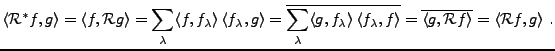
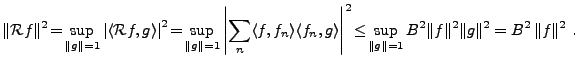
![]() étant auto adjoint, il résulte de (
étant auto adjoint, il résulte de (![[*]](crossref.png) )
que son spectre est inclus dans l'intervalle
)
que son spectre est inclus dans l'intervalle ![]() , ce
que l'on écrit aussi
, ce
que l'on écrit aussi
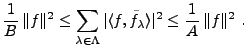
![]()
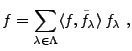
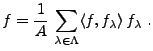
![[*]](crossref.png) ) pour expliciter un
) pour expliciter un 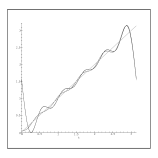
![]() défini en (
défini en (![[*]](crossref.png) ).
Il est possible de donner une caractérisation de l'image de
).
Il est possible de donner une caractérisation de l'image de ![]() par
par ![]() .
Dans le cas d'une base orthonormée
.
Dans le cas d'une base orthonormée
![]() de
de
![]() , le théorème de Riesz-Fisher établit une
correspondance bijective entre
, le théorème de Riesz-Fisher établit une
correspondance bijective entre
![]() et
et
![]() . Dans le
cas d'un repère, la suite
. Dans le
cas d'un repère, la suite ![]() des coefficients
des coefficients
![]() de
de
![]() est bien dans
est bien dans
![]() . Il résulte de la définition que
. Il résulte de la définition que ![]() est injectif,
et que
est injectif,
et que
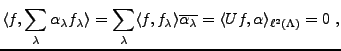
![]() , défini par
, défini par

![]() . Il admet une unique décomposition
. Il admet une unique décomposition
![]() , avec
, avec
![]() et
et
![]() . On suppose
. On suppose
![]() . Soit
. Soit ![]() un inverse à gauche de
un inverse à gauche de ![]() . Alors on a
. Alors on a
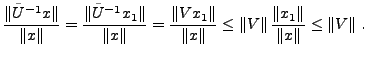
![[*]](crossref.png) ),
),
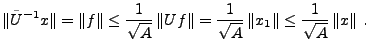
![]() possède un statut particulier,
comme le montre le corollaire suivant:
possède un statut particulier,
comme le montre le corollaire suivant:

![]() (où
(où
![]() ). On a
). On a ![]() , et il existe
, et il existe ![]() tel que
tel que
![]() , et
, et
![]() . Donc
il s'agit bien d'un projecteur orthogonal.
. Donc
il s'agit bien d'un projecteur orthogonal.
![]() . Donc,
. Donc,
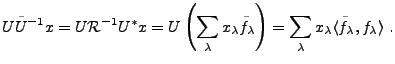
![]() est un multiple
de l'identité. La situation est un peu plus complexe dans le cas
général, puisqu'il faut utiliser la relation
est un multiple
de l'identité. La situation est un peu plus complexe dans le cas
général, puisqu'il faut utiliser la relation
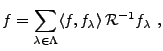
![]() . On sait que
. On sait que
![]() . Par conséquent, on a aussi
. Par conséquent, on a aussi