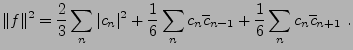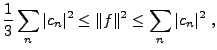Sous-sections
Rappels d'analyse fonctionnelle
Les outils de base pour l'analyse et le traitement des signaux
(déterministes comme aléatoires) sont les outils d'analyse
Hilbertienne, en dimension finie et infinie.
On rappelle dans ce chapitre les notions
élémentaires (espaces de Hilbert, bases orthonormées,...).
Ces notions sont utilisées pour la théorie 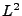 des séries
de Fourier.
des séries
de Fourier.
Commençons par rappeler quelques résultats élémentaires
concernant les espaces de Hilbert. Pour plus de détails, on
pourra se référer à tout texte de base, par exemple [7]

En posant pour tout 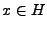
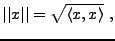 |
(A.1) |
on définit une norme sur  . On a alors les propriétés suivantes:
La norme munit
. On a alors les propriétés suivantes:
La norme munit  d'une structure d'espace métrique.
d'une structure d'espace métrique.

Le résultat suivant est une conséquence immédiate des inégalités
données ci-dessus.

Si
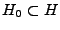 est un sous-espace de dimension finie de
est un sous-espace de dimension finie de
 , on note
, on note 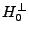 le sous-espace de
le sous-espace de  consistant
des
consistant
des 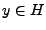 tels que
tels que
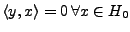 .
.

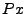 et
et 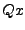 sont respectivement les projections orthogonales de
sont respectivement les projections orthogonales de
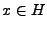 sur
sur 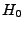 et
et 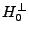 .
.
Preuve:
1) Unicité: supposons
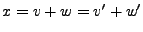 , avec
, avec
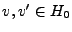 et
et
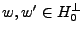 . Alors
. Alors 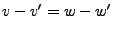 . Comme
. Comme
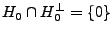 ,
ceci implique
,
ceci implique 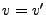 et
et 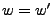 .
Existence: Soit
.
Existence: Soit
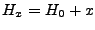 .
. 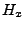 est convexe.
Il possède donc un élément de norme minimale,
noté
est convexe.
Il possède donc un élément de norme minimale,
noté 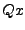 . Soit
. Soit 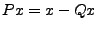 .
On vérifie immédiatement que
.
On vérifie immédiatement que 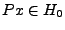 . Soit
. Soit
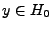 , avec
, avec 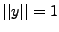 ; calculons
; calculons
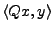 . Pour cela, soit
. Pour cela, soit
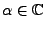 , et évaluons
, et évaluons
Si on prend
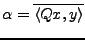 ,
cette dernière inégalité
implique que
,
cette dernière inégalité
implique que
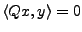 .
.
2)Soit 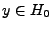 . Alors
. Alors
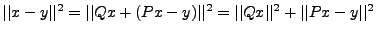 est
minimal pour
est
minimal pour 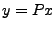 .
.
3) et 4) sont immédiats.

Le théorème suivant montre qu'un espace de Hilbert est
nécessairement isomorphe à son dual.

Preuve:
La première partie est une conséquence immédiate du
Théorème ![[*]](crossref.png) , et on se focalise sur la seconde
partie. Unicité: Supposons que
, et on se focalise sur la seconde
partie. Unicité: Supposons que
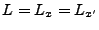 , pour
, pour  .
Alors
.
Alors
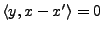 pour tout
pour tout 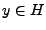 , donc
, donc 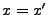 .
Existence: soit
.
Existence: soit
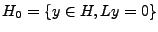 .
. 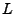 étant linéaire,
étant linéaire,
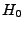 est un sous-espace de
est un sous-espace de  . De plus,
. De plus, 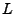 étant continue,
étant continue,
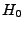 est fermé. Soit
est fermé. Soit
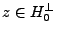 , avec
, avec  .
Soit
.
Soit
 . Clairement,
. Clairement, 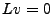 , et donc
, et donc
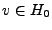 et
et
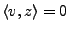 . Par conséquent,
. Par conséquent,
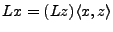 , et en posant
, et en posant
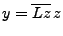 ,
on a bien
,
on a bien 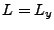 .
.

La façon la plus simple de décrire un espace de Hilbert
est d'utiliser une base. Plusieurs notions de bases Hilbertiennes
peuvent être introduites. L'une des plus générales est la notion de
base de Schauder. Une famille
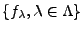 est une base de Schauder d'un espace de Banach
est une base de Schauder d'un espace de Banach 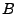 si
si
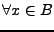 ,
il existe une unique suite
,
il existe une unique suite
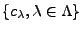 telle que
telle que
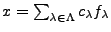 (dans le cas où
(dans le cas où 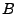 est de dimension infinie, l'égalité est à
prendre au sens de la topologie induite par la norme de
est de dimension infinie, l'égalité est à
prendre au sens de la topologie induite par la norme de 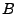 ).
Cependant, les bases de Schauder sont souvent difficiles à manipuler,
et la convergence du développement d'un élément de l'espace par rapport
à une telle base est parfois problématique. C'est pourquoi il est
utile de se limiter à des bases plus spécifiques. Le cas le plus simple
est le cas des bases orthonormales. Commençons par préciser
la notion d'orthogonalité et de projection orthogonale.
).
Cependant, les bases de Schauder sont souvent difficiles à manipuler,
et la convergence du développement d'un élément de l'espace par rapport
à une telle base est parfois problématique. C'est pourquoi il est
utile de se limiter à des bases plus spécifiques. Le cas le plus simple
est le cas des bases orthonormales. Commençons par préciser
la notion d'orthogonalité et de projection orthogonale.
Dans cette section,  est un espace de Hilbert séparable.
Un système orthonormal dans
est un espace de Hilbert séparable.
Un système orthonormal dans  est une famille
est une famille
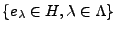 , telle que
, telle que
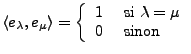 |
(A.2) |
Ici, 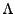 est un index au plus dénombrable
(si
est un index au plus dénombrable
(si 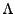 est infini, on prendra
est infini, on prendra
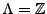 ).
).
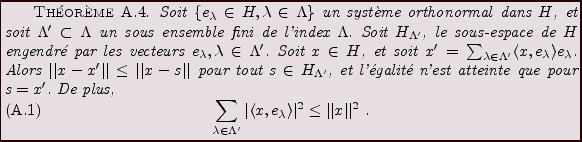
Preuve:
Pour tout
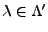 ,
,
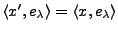 .
Donc,
.
Donc,
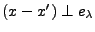 pour tout
pour tout
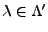 , et
, et
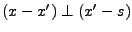 pour tout
pour tout
 . Donc,
. Donc,
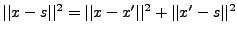 , et
, et
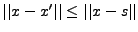 pour tout
pour tout
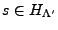 . De plus, cette inégalité
prise pour
. De plus, cette inégalité
prise pour 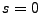 montre que
montre que
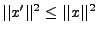 , ce qui conclut
la preuve.
, ce qui conclut
la preuve.

Ceci montre en particulier que 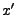 est la meilleure approximation
de
est la meilleure approximation
de 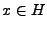 dans
dans 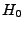 .
.
Le résultat suivant, appelé théorème de Riesz-Fischer,
permet de préciser le précédent. Il établit en particulier
le fait que l'existence d'une base orthonormée dans un espace de
Hilbert permet de le mettre en correspondance avec un espace
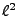 de suites de carré sommable.
de suites de carré sommable.
![\begin{theorem}[Riesz-Fischer]
Soit $\{e_\lambda,\lambda\in\Lambda\}$\ un syst\\lq ...
...om\'etrie de $\overline{F}$\ sur $\ell^2(\Lambda)$.
\end{enumerate}\end{theorem}](img1246.png)
Ce résultat est une conséquence du lemme classique suivant

Preuve:
Le fait que  se prolonge en une isométrie est une conséquence
immédiate de la densité de
se prolonge en une isométrie est une conséquence
immédiate de la densité de 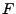 dans
dans 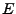 .
L'élément essentiel du résultat est la surjectivité. Soit
.
L'élément essentiel du résultat est la surjectivité. Soit
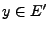 . Comme
. Comme  est dense dans
est dense dans 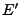 , il existe une suite
, il existe une suite
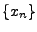 d'éléments de
d'éléments de 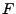 telle que
telle que
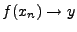 .
La suite
.
La suite
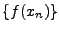 est une suite de Cauchy, et
est une suite de Cauchy, et  étant une
isométrie, la suite
étant une
isométrie, la suite 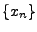 est elle aussi une suite de Cauchy,
qui converge vers
est elle aussi une suite de Cauchy,
qui converge vers 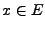 (puisque
(puisque 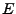 est complet).
est complet).  étant continue,
on a bien
étant continue,
on a bien 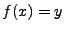 , ce qui prouve le lemme.
, ce qui prouve le lemme.

Preuve du théorème ![[*]](crossref.png) :
L'inégalité (
:
L'inégalité (![[*]](crossref.png) ) est vraie pour tout
sous-ensemble fini de
) est vraie pour tout
sous-ensemble fini de 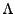 , et implique donc
l'inégalité de Bessel.
On considère l'application ``coefficients''
, et implique donc
l'inégalité de Bessel.
On considère l'application ``coefficients''  , qui à
, qui à 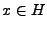 associe
la suite des coefficients
associe
la suite des coefficients
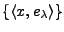 .
.  est
bien entendu linéaire; d'après l'inégalité de Bessel, on a
pour tous
est
bien entendu linéaire; d'après l'inégalité de Bessel, on a
pour tous 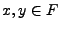 :
:
et  est donc continue de
est donc continue de 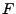 dans
dans
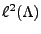 . Il suffit
alors d'appliquer le Lemme
. Il suffit
alors d'appliquer le Lemme ![[*]](crossref.png) pour conclure.
pour conclure.


Le résultat suivant donne une caractérisation des bases orthonormées.
Rappelons qu'une famille
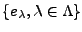 est
complète dans
est
complète dans  si l'ensemble des combinaisons linéaires
finies des
si l'ensemble des combinaisons linéaires
finies des 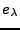 est dense dans
est dense dans  .
.
REMARQUE A..1 On parle parfois de famile
totale au lieu de
famille complète. Les deux terminologies décrivent la même notion.
On montre que dans un espace de Hilbert, une famille
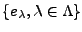
est complète si
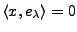
pour tout
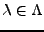
implique
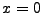
.

Preuve:
1) implique 2): soit 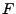 l'ensemble des combinaisons linéaires
finies des
l'ensemble des combinaisons linéaires
finies des 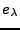 , et supposons
, et supposons
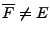 . Alors,
il existe
. Alors,
il existe
 ,
, 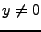 , et la famille
n'est pas maximale. Les autres implications sont des conséquences
directes des résultats précédents. 2) implique 3): c'est une
conséquence du théorème de Riesz-Fischer ci-dessus.
3) implique 4): s'obtient grâce à l'identité de polarisation.
4) implique 1): supposons que 1) soit faux: il existe
, et la famille
n'est pas maximale. Les autres implications sont des conséquences
directes des résultats précédents. 2) implique 3): c'est une
conséquence du théorème de Riesz-Fischer ci-dessus.
3) implique 4): s'obtient grâce à l'identité de polarisation.
4) implique 1): supposons que 1) soit faux: il existe 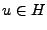 ,
, 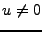 ,
tel que
,
tel que
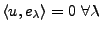 .
Alors, d'après 4),
.
Alors, d'après 4), 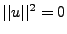 , ce qui est impossible.
, ce qui est impossible.

EXEMPLE A..1 En dimension finie, par exemple pour
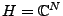
, toute famille
orthonormale de
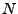
vecteurs est une base orthonormée.
EXEMPLE A..2 Considérons l'espace
muni du produit scalaire usuel sur

. En posant
on vérifie que la famille des
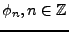
est une base orthonormée de
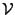
. L'orthonormalité des
fonctions
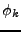
est immédiate. Par ailleurs, si

est
orthogonale à toutes les fonctions
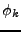
, alors

est nulle sur tout
intervalle
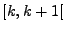
et est donc nulle.
EXEMPLE A..3 Soit la function
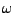
définie par
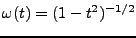
. On considère l'espace
![$ L^2_\omega([-1,1])$](img1280.png)
des fonctions

telles que
![$ f\sqrt{\omega}\in L^2([-1,1])$](img1281.png)
.
![$ L^2_\omega([-1,1])$](img1280.png)
est muni d'une structure d'espace de Hilbert par le produit Hermitien
Soit
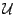
l'opérateur défini par
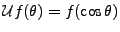
.
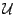
est une isométrie de
![$ L^2_\omega([-1,1])$](img1280.png)
sur
![$ L^2([0,\pi])$](img1285.png)
:
On sait que la famille des fonctions

définies par
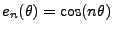
est une base orthogonale de
![$ L^2([0,\pi])$](img1285.png)
.
Par conséquent, la famille des fonctions

:
est une base orthogonale de
![$ L^2_\omega([-1,1])$](img1280.png)
. Les fonctions
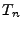
sont appelées
polynômes de Chebyshev.
Jusqu'à présent, nous nous sommes limités à utiliser
des bases orthonormées, qui ont le grand mérite de
simplifier la représentation des signaux (grâce en
particulier au théorème de Riesz-Fischer, et à la formule
de Parseval).
Par malheur, il n'est pas toujours facile de construire
directement une base orthonormée de l'espace considéré.
Il est alors utile de commencer par une base de Riesz,
comme définie ci-dessous.

Remarquons immédiatement que si
 est
une base de Riesz de
est
une base de Riesz de  , alors on a
, alors on a
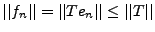 .
De même, on déduit de
.
De même, on déduit de
 que
que
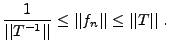 |
(A.3) |
Le résultat suivant donne une caractérisation des
bases de Riesz.

Preuve:
1 implique 2:
supposant que
 soit
une base de Riesz de
soit
une base de Riesz de  , il existe
, il existe 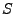 , borné, inversible à inverse
borné, tel que pour tout
, borné, inversible à inverse
borné, tel que pour tout 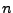 ,
, 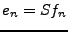 . Soit
. Soit
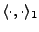 défini par
défini par
On vérifie immédiatement que la famille 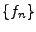 est
orthonormale par rapport à ce produit scalaire. De plus, on a
est
orthonormale par rapport à ce produit scalaire. De plus, on a
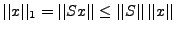 , et
, et
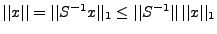 . Donc les
produits scalaires sont équivalents.
. Donc les
produits scalaires sont équivalents.
2 implique 3:
soit
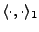 le produit
scalaire équivalent; soit
le produit
scalaire équivalent; soit 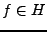 telle
que
telle
que
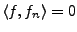 pour tout
pour tout 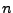 . Alors, on a
. Alors, on a
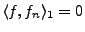 pour tout
pour tout 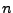 , ce qui implique
, ce qui implique 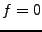 .
donc la famille
.
donc la famille 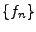 est complète. Soit maintenant
est complète. Soit maintenant 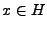 .
On sait que
.
On sait que
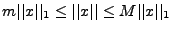 , où
, où 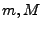 sont deux
constantes indépendantes de
sont deux
constantes indépendantes de 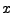 . Si on prend un
. Si on prend un 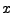 de la forme
de la forme
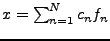 , alors
, alors
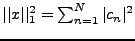 et on a immédiatement la propriété annoncée.
et on a immédiatement la propriété annoncée.
3 implique 1:
Soit 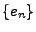 une base orthonormée de
une base orthonormée de  . Alors, il existe deux
opérateurs linéaires
. Alors, il existe deux
opérateurs linéaires  , bornés grâce à (
, bornés grâce à (![[*]](crossref.png) ),
tels que pour tout
),
tels que pour tout  ,
, 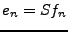 et
et 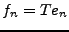 . Donc
. Donc
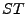 est l'opérateur identité sur
est l'opérateur identité sur  . Mais la famille
. Mais la famille 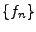 étant complète,
étant complète, 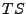 est aussi l'identité sur
est aussi l'identité sur  . Donc
. Donc
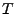 est inversible, ce qui conclut la preuve.
est inversible, ce qui conclut la preuve.

REMARQUE A..2 Une base de Riesz possède automatiquement une
base biorthogonale
(ou base duale)
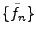
, telle que
qui est également une base de Riesz du même espace. En effet,
avec les notations plus haut, considérons l'adjoint
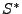
de
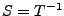
,
et posons
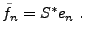 |
(A.4) |
Alors on a immédiatement
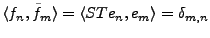
.
De plus, pour tous
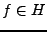
, on peut écrire
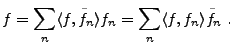 |
(A.5) |
Par exemple, en écrivant
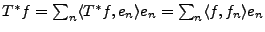
, on obtient directement la seconde
égalité. La première s'obtient similairement en décomposant
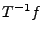
sur la base
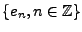
. Le fait que
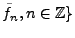
est
une conséquence directe des propriétés de
.
Bruno Torresani
2007-06-26
![]() des séries
de Fourier.
des séries
de Fourier.


![]() , avec
, avec
![]() et
et
![]() . Alors
. Alors ![]() . Comme
. Comme
![]() ,
ceci implique
,
ceci implique ![]() et
et ![]() .
Existence: Soit
.
Existence: Soit
![]() .
. ![]() est convexe.
Il possède donc un élément de norme minimale,
noté
est convexe.
Il possède donc un élément de norme minimale,
noté ![]() . Soit
. Soit ![]() .
On vérifie immédiatement que
.
On vérifie immédiatement que ![]() . Soit
. Soit
![]() , avec
, avec ![]() ; calculons
; calculons
![]() . Pour cela, soit
. Pour cela, soit
![]() , et évaluons
, et évaluons
![]() . Alors
. Alors
![]() est
minimal pour
est
minimal pour ![]() .
.
![]()

![[*]](crossref.png) , et on se focalise sur la seconde
partie. Unicité: Supposons que
, et on se focalise sur la seconde
partie. Unicité: Supposons que
![]() , pour
, pour ![]() .
Alors
.
Alors
![]() pour tout
pour tout ![]() , donc
, donc ![]() .
Existence: soit
.
Existence: soit
![]() .
. ![]() étant linéaire,
étant linéaire,
![]() est un sous-espace de
est un sous-espace de ![]() . De plus,
. De plus, ![]() étant continue,
étant continue,
![]() est fermé. Soit
est fermé. Soit
![]() , avec
, avec ![]() .
Soit
.
Soit
![]() . Clairement,
. Clairement, ![]() , et donc
, et donc
![]() et
et
![]() . Par conséquent,
. Par conséquent,
![]() , et en posant
, et en posant
![]() ,
on a bien
,
on a bien ![]() .
.
![]()
![]() est un espace de Hilbert séparable.
Un système orthonormal dans
est un espace de Hilbert séparable.
Un système orthonormal dans ![]() est une famille
est une famille
![]() , telle que
, telle que
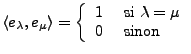
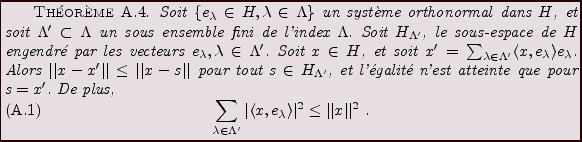
![]() est la meilleure approximation
de
est la meilleure approximation
de ![]() dans
dans ![]() .
.
![]() de suites de carré sommable.
de suites de carré sommable.
![\begin{theorem}[Riesz-Fischer]
Soit $\{e_\lambda,\lambda\in\Lambda\}$\ un syst\\lq ...
...om\'etrie de $\overline{F}$\ sur $\ell^2(\Lambda)$.
\end{enumerate}\end{theorem}](img1246.png)

![]() se prolonge en une isométrie est une conséquence
immédiate de la densité de
se prolonge en une isométrie est une conséquence
immédiate de la densité de ![]() dans
dans ![]() .
L'élément essentiel du résultat est la surjectivité. Soit
.
L'élément essentiel du résultat est la surjectivité. Soit
![]() . Comme
. Comme ![]() est dense dans
est dense dans ![]() , il existe une suite
, il existe une suite
![]() d'éléments de
d'éléments de ![]() telle que
telle que
![]() .
La suite
.
La suite
![]() est une suite de Cauchy, et
est une suite de Cauchy, et ![]() étant une
isométrie, la suite
étant une
isométrie, la suite ![]() est elle aussi une suite de Cauchy,
qui converge vers
est elle aussi une suite de Cauchy,
qui converge vers ![]() (puisque
(puisque ![]() est complet).
est complet). ![]() étant continue,
on a bien
étant continue,
on a bien ![]() , ce qui prouve le lemme.
, ce qui prouve le lemme.
![]()
![[*]](crossref.png) :
L'inégalité (
:
L'inégalité (![[*]](crossref.png) ) est vraie pour tout
sous-ensemble fini de
) est vraie pour tout
sous-ensemble fini de ![]() , et implique donc
l'inégalité de Bessel.
On considère l'application ``coefficients''
, et implique donc
l'inégalité de Bessel.
On considère l'application ``coefficients'' ![]() , qui à
, qui à ![]() associe
la suite des coefficients
associe
la suite des coefficients
![]() .
. ![]() est
bien entendu linéaire; d'après l'inégalité de Bessel, on a
pour tous
est
bien entendu linéaire; d'après l'inégalité de Bessel, on a
pour tous ![]() :
:
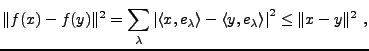
![[*]](crossref.png) pour conclure.
pour conclure.
![]()
![]() est
complète dans
est
complète dans ![]() si l'ensemble des combinaisons linéaires
finies des
si l'ensemble des combinaisons linéaires
finies des ![]() est dense dans
est dense dans ![]() .
.

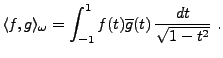
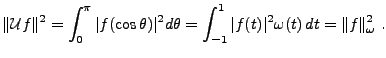

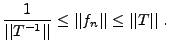

![[*]](crossref.png) ),
tels que pour tout
),
tels que pour tout ![$\displaystyle \Lambda(t) = \left\{\begin{array}{ll}
t&\hbox{ si }t\in [0,1]\\
2-t&\hbox{ si }t\in [1,2]\\
0&\hbox{ sinon}\ ,
\end{array}\right.
$](img1315.png)