Next: Problèmes hyperboliques: phénomènes de Up: Equations aux dérivées partielles Previous: Problèmes elliptiques: le Laplacien
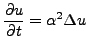 |
(3.22) |
Comme on l'a vu, le Laplacien mesure la convexité d'une fonction.
Si
![]() , alors
, alors
![]() est inférieure à sa
moyenne sur un petit voisinage de
est inférieure à sa
moyenne sur un petit voisinage de
![]() ; alors
; alors
![]() , ce qui
va faire augmenter la valeur de
, ce qui
va faire augmenter la valeur de
![]() . Inversement, si
. Inversement, si
![]() , alors la valeur de
, alors la valeur de
![]() va diminuer.
Ce type d'équation a donc tendance à moyenner, ou ``lisser''
la solution au cours du temps.
va diminuer.
Ce type d'équation a donc tendance à moyenner, ou ``lisser''
la solution au cours du temps.
Comme autre exemple d'équation parabolique, on peut notamment mentionner l'équaqion de convection-diffusion, que l'on obtient en ajoutant un terme de convection à l'équation de la chaleur
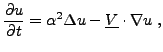
Les EDP de cette classe peuvent être considérées dans l'espace
tout entier, ou dans un domaine borné de l'espace, ce qui donne lieu
soit à des conditions au bord, soit des conditions aux limites
(dans ce cas on impose en général que la solution tende vers
zéro à l'infini). La variable temporelle est
en général prise dans
![]() , et on complète le problème par
des conditions initiales.
, et on complète le problème par
des conditions initiales.
Il arrive toutefois que les conditions aux bords portent sur le flux, c'est à dire la dérivée normale de la solution sur le bord. On parle alors de condition de Neumann
Les conditions au bord mixtes apparaissent assez couramment, notamment dans les problèmes de conduction de la chaleur, pour lesquels la dérivée normale est proportionnelle à la différence entre la valeur de la solution à l'intérieur du domaine et sa valeur à l'extérieur.
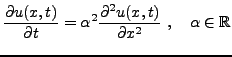 |
(3.26) |
| (3.27) |
On recherche en général des solutions par la méthode de séparation des variables, c'est à dire sous la forme
Sous cette forme, on se ramène alors à une équation de la forme
où encore
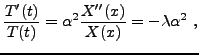
L'équation temporelle conduit directement à
ce qui force
elle conduit à des solutions de la forme
Pour aller plus loin, il faut imposer les conditions aux bords. On se limitera ici aux daux types de conditions aux bords les plus courantes, c'est à dire les conditions de Dirichlet et les conditions mixtes de Robin.
Ceci correspond à une situation physique décrite dans la figure
![[*]](crossref.png) : une barre conductrice de
la chaleur, dont les deux extrémités sont maintenues à
température nulle par un thermostat, et isolée latéralement.
: une barre conductrice de
la chaleur, dont les deux extrémités sont maintenues à
température nulle par un thermostat, et isolée latéralement.
Cette condition au bord conduit à
La première équation donne
Si on évite la solution nulle, ceci implique que les seules solutions pour
| (3.29) |
et plus généralement, l'équation et les conditions aux bords étant homogènes, une solution générale
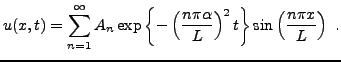
La dernière étape consiste à trouver les valeurs des constantes
![]() . On utilise pour cela la condition initiale, qui prend donc la
forme
. On utilise pour cela la condition initiale, qui prend donc la
forme
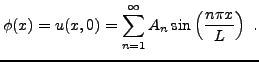
Restent à trouver les constantes
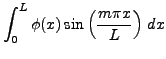 |
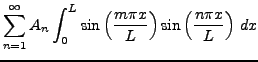 |
||
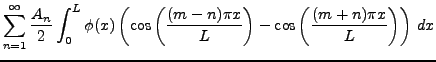 |
|||

La manière dont on a retrouvé les coefficients ![]() peut sembler
un peu arbitraire. En fait, elle provient du résultat suivant, qui
suggère donc le calcul fait pour retrouver les
peut sembler
un peu arbitraire. En fait, elle provient du résultat suivant, qui
suggère donc le calcul fait pour retrouver les ![]() :
:
![\begin{lemma}
La famille de fonctions
\begin{equation}
e_n: x\in [0,L]\to e_n(x)...
...r\'e int\'egrable sur $[0,L]$\ qui s'annulent en $x=0$\ et en $x=L$.
\end{lemma}](img750.png)
en imposant des conditions au bord particulières. Or nous avons vu au chapitre
![[*]](crossref.png) que ces problèmes de Sturm-Liouville
fournissent des bases orthonormées d'espaces de Hilbert adaptés
aux conditions aux bords choisies. Le lemme ci-dessus se place
donc précisément dans ce cadre.
que ces problèmes de Sturm-Liouville
fournissent des bases orthonormées d'espaces de Hilbert adaptés
aux conditions aux bords choisies. Le lemme ci-dessus se place
donc précisément dans ce cadre.
On considère ici la situation décrite dans la
figure ![[*]](crossref.png) , d'une barre conductrice isolée
latéralement, dont le côté gauche est maintenu à température
nulle, et le droit est en contact avec un milieu se trouvant lui aussi à
température nulle.
, d'une barre conductrice isolée
latéralement, dont le côté gauche est maintenu à température
nulle, et le droit est en contact avec un milieu se trouvant lui aussi à
température nulle.
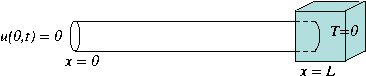
|
Le calcul de la solution générale est le même que plus haut,
jusqu'à l'équation (![[*]](crossref.png) ). On doit maintenant
utiliser la condition au bord, que l'on doit cette fois choisir
de type Dirichlet à gauche, et mixte à droite
). On doit maintenant
utiliser la condition au bord, que l'on doit cette fois choisir
de type Dirichlet à gauche, et mixte à droite
La première condition implique comme précédemment
Comme précédemment, les valeurs possibles de
d'où les valeurs possibles de
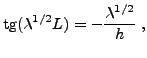 |
(3.30) |
![[*]](crossref.png) . Les valeurs admissibles
de
. Les valeurs admissibles
de
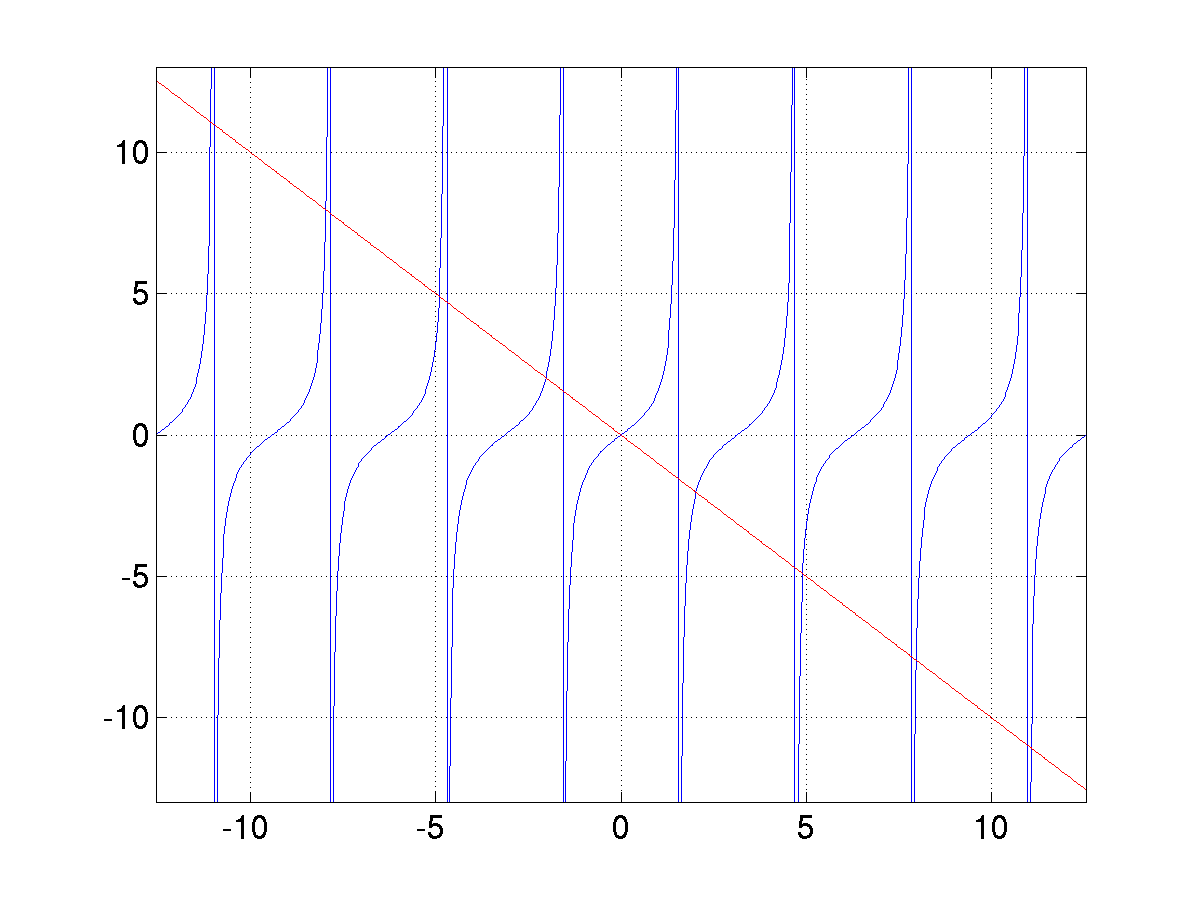
|
La solution générale du problème considéré est donc de la forme
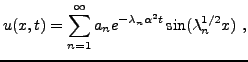 |
(3.31) |
![\begin{lemma}
La famille de fonctions
\begin{equation}
f_n: x\in [0,L]\to f_n(x)...
...]), f(0)=0\ \mathrm{et}\ f'(L) + hf(L)=0\right\}\ .
\end{displaymath}\end{lemma}](img761.png)
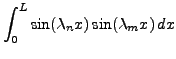 |
![$\displaystyle \left[-\frac1{\lambda_m}\sin(\lambda_n x)\cos(\lambda_m x)\right]_0^L
+ \frac{\lambda_n}{\lambda_m}
\int_0^L \cos(\lambda_n x)\cos(\lambda_m x)\,dx$](img763.png) |
||
![$\displaystyle -\frac1{\lambda_m}\sin(\lambda_n L)\cos(\lambda_m L) +
\frac{\lam...
...bda_m}\bigg\{\left[\frac{\sin(\lambda_m
x)}{\lambda_m} \cos(\lambda_n x)\right]$](img764.png) |
|||
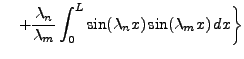 |
|||
![$\displaystyle -\frac1{\lambda_m}\bigg\{
\sin(\lambda_nL)\cos(\lambda_mL) - [-h\sin(\lambda_n
L)][-\cos(\lambda_m L)/h]\bigg\}$](img766.png) |
|||
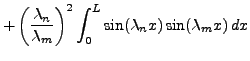 |
|||
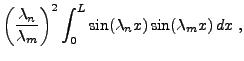 |
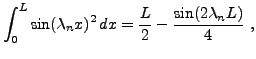
ce qui conclut la preuve.
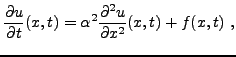
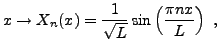
pour décomposer le terme source
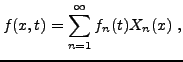
et de là développer un calcul similaire au précédent.
Bruno Torresani 2007-06-26