Quelques exemples... et contre-exemples simples

Le brachistrochrone

Figure: Trajet le plus court (en temps) d'un point à un autre: trois trajectoires possibles, plus ou moins vraisemblables.

On considère un mobile de masse $m$ , asujetti à glisser sans frottement sur une surface inclinée reliant un point initial $A$ de coordonnées $(x_1,z_1)$ à un point final $B$ de coordonnées $(x_2,z_2)$ , utilisant la seule force de la pesanteur. On suppose que la vitesse initiale du mobile est nulle, et on cherche la forme de la surface inclinée (donc la trajectoire du mobile) qui conduira au trajet le plus court en temps.

On note $x$ la variable horizontale, qui sera notre variable indépendante, et $z = z(x)$ la variable verticale (dépendante), orientée vers le bas. On choisit le système de coordonnées de sorte que $A$ soit placé à l'origine des abscisses et des côtes. L'énergie cinétique et l'énergie potentielle valent respectivement

$$T = \frac1{2}mv^2\ ,\qquad V = -mgz + C\ .$$

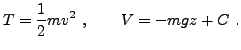
La conservation de l'énergie totale implique que

$$E = T+V = C$$

de sorte que la vitesse varie avec l'altitude comme

$$v(z) = \sqrt{2gz}\ .$$

Le temps total nécessaire pour le trajet $x\in [x_1,x_2]\to z(x)$ vaut

$$\Phi[z] = \int_{x_1}^{x_2} \frac{ds(x)}{v(z(x))} = \frac1{\sqrt{2g}} \int_{x_1}^{x_2} \frac{\sqrt{1+z'(x)^2}}{\sqrt{z(x)}}\, dx$$

On est bien dans le cas de l'équation de Beltrami (pas de dépendance explicite de $F$ dans la variable indépendante $x$ ), qui s'écrit donc

$$\frac{z'(x)^2}{\sqrt{z(x)(1+z'(x)^2)}} - \frac{\sqrt{1+z'(x)^2}}{\sqrt{z(x)}} = C\ .$$

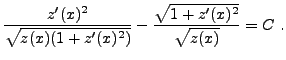
Quelques manipulations donnent

$$C^2 z(x)\left(1+z'(x)^2\right) =1\ ,$$

d'où, en posant $k=1/C^2$ ,

$$\frac{dz}{dx}(x) = \sqrt{\frac{k-z(x)}{z(x)}}\ .$$

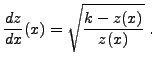
Remarquons que $C^2z\le 1$ , donc $0\le z\le k$ . On pose $\sqrt{(k-z)/z}=\mathrm{cotan}\phi$ , d'où on peut déduire $z=k\sin^2\phi$ .

Pour exprimer $x$ en fonction de $\phi$ , calculons

$$\frac{dx}{d\phi} =\frac{dx}{dz}\frac{dz}{d\phi} = 2k\sin^2\phi = k[1-\cos(2\phi)]\ .$$

Ainsi, on en déduit (puisque pour $x=0$ on a aussi $z=0$ )

$$x = k\left(\phi - \sin(2\phi)/2\right)\ ,$$

d'où on tire une forme paramétrique de la solution

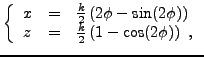$$\left\{ \begin{array}{lll} x &=& \frac{k}2\left(2\phi - \sin(2\phi)\right)\\ z &=& \frac{k}2\left(1 - \cos(2\phi)\right)\ , \end{array} \right.$$ (1.8)

ce qui est l'équation paramétrique d'une cycloïde. On peut éliminer le paramètre $\phi$ , en posant $a=k/2$ , et en remarquant que

$$2\phi = \cos{^{-1}}\left(\frac{a-z}a\right)\ ,$$

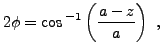
puis en insérant dans l'équation de $x$

$$x(z) = a \cos{^{-1}}\left(\frac{a-z}a\right) - a \sqrt{1 - \left(... ...{a-z}a\right)^2} = a \cos{^{-1}}\left(\frac{a-z}a\right) - \sqrt{2az -z^2}\ .$$

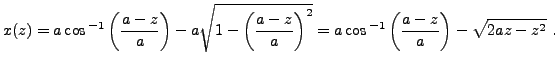
La valeur numérique de $a$ est alors déterminée par la condition limite $x(z_2)=x_2$ .

Figure: La cycloïde.

Le Principe de Fermat

Retour sur les lois de Snell-Descartes, dans un cas où l'indice (et donc la vitesse de propagation de la lumière) dépend de la position: le problème des mirages, illustré en FIG.  et FIG. 

Figure: Le phénomène du mirage: deux trajectoires de lumière du ciel (traits pleins); la trajectoire du bas est courbée par un gradient de densité (dû, par exemple, à un gradient de température); l'oeil perçoit une image virtuelle au sol, qui est en fait une image du ciel.

Figure: Un vrai mirage

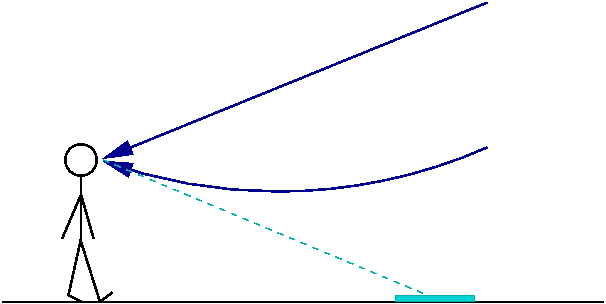
Le temps de trajet dépend du chemin choisi; en prenant $y = y(x)$ , ou alternativement $x=x(y)$ , on obtient pour le temps de trajet de la lumière entre deux points l'expression suivante

$$\int n ds = \int f(y) ds = \int f(y) \sqrt{1+x'(y)^2} dy= \int f(y) \sqrt{1+y'(x)^2} dx\ .$$

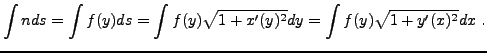
On privilégie $y$ comme variable indépendante, car on n'a ainsi pas de d'ependance explicite dans la variable dépendante $x$ , ce qui simplifie l'équation d'Euler-Lagrange. Celle-ci donne

$$f(y) \frac{x'}{\sqrt{1+x'^2}} = C\ ,$$

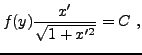
c'est à dire

$$x' = \frac{C}{\sqrt{f(y)^2-C^2}}\ .$$

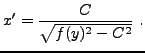
Pour aller plus loin, il est temps de faire un choix pour la variation de l'indice en fonction de l'altitude. Supposons une dépendance linéaire. Le choix particulier $f(y) = n_0 (1+\alpha y)$ donne

$$dx = \frac{C}{\alpha n_0} \frac{dy}{\sqrt{(y+1/\alpha)^2 + (C/\alpha n_0)^2}}$$

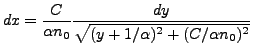
en posant $u=y+1/\alpha=(C/\alpha n_0){\rm ch}\theta$ on obtient $dy = \frac{C}{\alpha n_0} {\rm sh}\theta\,d\theta$ , d'où

$$dx = \left(\frac{C}{\alpha n_0}\right)^2 \frac{{\rm sh}\theta\,d\... ...n_0)^2{\rm ch}^2\theta - (C/\alpha n_0)^2}} = \frac{C}{\alpha n_0}\,d\theta\ ,$$

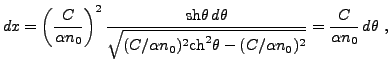
et finalement, une simple intégration donne $\theta = (\alpha n_0/C)(x-x_0)$ , d'où

$$y=-\frac1{\alpha} + \frac{C}{\alpha n_0}{\rm ch}((\alpha n_0/C)(x-x_0))\ .$$

Il s'agit d'une chaînette, ou caténoïde, que l'on peut approximer par une parabole au second ordre, autour de $x_0$ . Les constantes d'intégration $x_0$ et $C$ peuvent être déterminées en considérant les conditions aux bords.

L'erreur de Lagrange

Les équations d'Euler-Lagrange que nous avons dérivées plus haut donnent des conditions nécessaires que doit satisfaire l'optimum de la fonctionnelle considérée, sous l'hypothèse que celui-ci soit deux fois différentiable. Il existe des problèmes pour lesquels cette hypothèse n'est pas adaptée, au sens où il existe des solutions $f$ ne la satisfaisant pas, mais donnant à la fonctionnelle une valeur meilleure que la meilleure solution deux fois différentiable.

Un exemple célèbre est donné par un problème étudié par Lagrange en 1783 (initialement formulé par Euler en 1744 puis Bernoulli): trouver la forme optimale d'une colonne de hauteur et volume fixés, pouvant supporter une pression maximale au sommet. Lagrange a eu le grand mérite de donner une formulation mathématique précise au problème, mais la solution qu'il proposa, et qui le conduit à une colonne cylindrique, était entâchée d'un certain nombre d'erreur, en particulier une hypothèse de différentiabilité de la solution. Il a en fait fallu attendre 1992 (après plusieurs tentatives, chacune marquée par des erreurs dues à des hypothèses inadaptées) pour que Cox et Overton aboutissent à une solution rigoureuse à ce problème, qui s'est ainsi avéré bien plus difficile qu'il n'y paraissait.

Figure: Le problème d'Euler-Bernoulli, la solution de Lagrange (à gauche) et la solution de Cox et Overton (à droite)