Subsections
Le cas que nous avons considéré est en fait le cas le plus simple,
qui peut être généralisé de diverses manières. Les cas
d'intérêt les plus classiques concernent les situations
multidimensionnelles, ainsi que les cas de fonctionnelles dépendant
de plusieurs fonctions.
La généralisation la plus immédiate concerne l'extension au cas d'une
variable indépendante
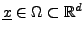 vectorielle:
la fonctionnelle
vectorielle:
la fonctionnelle
 considérée dépend alors des dérivées partielles
de
considérée dépend alors des dérivées partielles
de  par rapport aux différentes composantes de
par rapport aux différentes composantes de 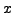 .
Pour simplifier, on notera
.
Pour simplifier, on notera
la dérivée partielle de la fonction  par rapport à la variable
par rapport à la variable
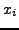 ,
,
et ainsi de suite.
Prenons l'exemple bidimensionnel: on se donne un domaine du plan
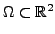 , dont on note
, dont on note
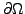 le bord, et
on recherche les extrêma
le bord, et
on recherche les extrêma
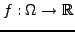 de la fonctionnelle
de la fonctionnelle  définie par
définie par
Comme dans le cas plus simple, on doit étudier les variations de  dans les ``directions''
dans les ``directions'' 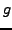
en se limitant aux fonctions 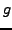 telles que
telles que
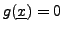 pour tout
pour tout
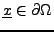 .
En suivant pas à pas le calcul précédent, on aboutit à
.
En suivant pas à pas le calcul précédent, on aboutit à
et une intégration par parties dans chacun des deux derniers termes,
prenant en compte le fait que  sur
sur
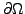 conduit à
conduit à
Il suffit alors d'utiliser le lemme fondamental du calcul des variations
(voir le lemme ![[*]](crossref.png) ), pour en déduire
), pour en déduire
Plus généralement, on montre le résultat suivant
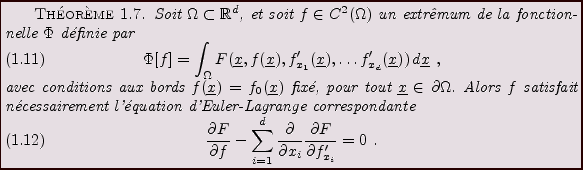
On obtiend donc un résultat qui est une généralisation
directe du Théorème ![[*]](crossref.png) .
.
On considère ci-dessous un certain nombre d'exemples d'applications de ce
résultat.
Surfaces minimales
Le problème de Plateau (ou du film de savon)
:
que se passe-t-il lorsque l'on plonge un anneau de forme quelconque
dans de l'eau savonneuse ? Un film de savon se forme à l'intérieur
de l'anneau, représentant une surface. La forme de cette surface
peut être calculée, partant du principe que la nature
cherche à minimiser l'aire de la surface ainsi créée.
On modélise cela de la façon suivante.
on considère un domaine
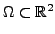 du plan, de bord
du plan, de bord
 et la hauteur du film de savon au point
et la hauteur du film de savon au point
 est notée
est notée
 ,
,
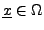 .
L'anneau est modélisé comme une fonction
.
L'anneau est modélisé comme une fonction
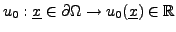 , et la surface
du film de savon représenté par
, et la surface
du film de savon représenté par 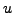 s'écrit comme
s'écrit comme
![$\displaystyle \Phi[u] = \int_\Omega \sqrt{1 + u'_{x_1}({\underline{x}})^2 + u'_{x_2}({\underline{x}})^2}\,d{\underline{x}}\ .$](img184.png) |
(1.9) |
Le problème posé est donc de minimiser  , avec la condition
au bord
, avec la condition
au bord
On a donc
fonction qui ne dépend explicitement ni de la variable
indépendante ni de 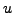 . Donc
Calculons
. Donc
Calculons
et une expression similaire pour la dérivée par rapport à
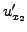 .
Calculons maintenant
.
Calculons maintenant
et une expression similaire pour
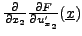 .
.
L'équation d'Euler-Lagrange associée
prend donc la forme
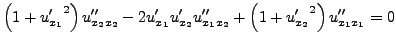 |
(1.10) |
On cherche à déterminer le champ électromagnétique à
l'intérieur d'un domaine
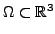 , dont les bords
sont fixés à un potentiel
, dont les bords
sont fixés à un potentiel 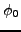 .
On note
.
On note 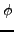 le potentiel dont dérive le champ électrique
le potentiel dont dérive le champ électrique 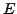 .
.
L'énergie électromagn étique engendrée par un
potentiel 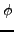 quelconque dans un volume
quelconque dans un volume
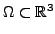 est de la forme
est de la forme
avec
Pour un potentiel aux bords fixé, le potentiel intérieur
est celui qui minimise cette énergie.
En variant ![$ W[\phi]$](img198.png) par rapport à
par rapport à 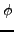 , avec conditions
aux bords fixées
, avec conditions
aux bords fixées
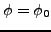 sur
sur
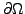 , on
obtient l'équation d'Euler-Lagrange
, on
obtient l'équation d'Euler-Lagrange
C'est l'équation de Laplace.
En l'absence de conditions aux bords,
un potentiel nul (et donc un champ nul) serait une solution, ce qui
n'est évidemment plus le cas en présence de conditions aux bords.
Soit
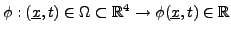 une fonction de l'espace et du temps, représentant la valeur
d'un champ (scalaire) au point
une fonction de l'espace et du temps, représentant la valeur
d'un champ (scalaire) au point
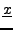 et à l'instant
et à l'instant 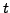 .
On suppose que l'énergie associée à ce champ
.
On suppose que l'énergie associée à ce champ 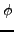 coïncide avec l'intégrale de la (pseudo)norme de Minkowsky
du quadrivecteur des dérivées spatiales et temporelle
du champ:
coïncide avec l'intégrale de la (pseudo)norme de Minkowsky
du quadrivecteur des dérivées spatiales et temporelle
du champ:
En minimisant cette quantité par rapport à 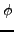 avec une condition aux bords donnée
avec une condition aux bords donnée
Il est facile de voir, par un calcul similaire au précédent,
que l'équation d'Euler-Lagrange correspondante est alors
l'équation des ondes
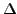 représentant le Laplacien spatial.
Une autre extension possible est celle au cas de fonctionnelles
non plus d'une mais de plusieurs variables dépendantes.
Contrairement à la section précédente, c'est maintenant la
variable dépendante qui est ici vectorielle, et non plus
la variable indépendante.
représentant le Laplacien spatial.
Une autre extension possible est celle au cas de fonctionnelles
non plus d'une mais de plusieurs variables dépendantes.
Contrairement à la section précédente, c'est maintenant la
variable dépendante qui est ici vectorielle, et non plus
la variable indépendante.
Par exemple, supposons que  s'écrive sous la forme
s'écrive sous la forme
Pour trouver les extrêma d'une telle fonctionnelle, c'est à dire les
couples 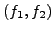 qui la minimisent ou la maximisent, il faut faire
varier simultanément
qui la minimisent ou la maximisent, il faut faire
varier simultanément 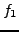 et
et 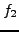 .
.
Il est facile de vérifier que dans un tel cas de figure, on obtient non plus
une mais deux équations d'Euler-Lagrange, donc un système
d'équations de la forme
Dans le cas de dimension quelconque, on montre similairement
le résultat suivant

EXEMPLE 1.6 La mécanique Hamiltonienne fournit de nombreux exemples de
telles situations. Notons par exemple
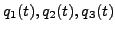
les coordonnées d'un point matériel à l'instant
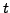
,
et
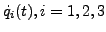
les dérivées temporelles de ces
coordonnées. Si on note
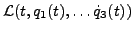
la densité
Lagrangienne associée, alors les trajectoires entre
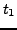
et
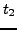
sont données par les minima de l'intégrale d'action
L'équation de Beltrami (Proposition ![[*]](crossref.png) ) se généralise
elle aussi de façon simple. Supposons que la fonction
) se généralise
elle aussi de façon simple. Supposons que la fonction 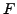 ne dépende pas
explicitement de la variable dépendante
ne dépende pas
explicitement de la variable dépendante 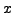 , on peut
alors écrire (en omettant les variables, pour simplifier les écritures)
pour tout
, on peut
alors écrire (en omettant les variables, pour simplifier les écritures)
pour tout 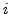
Partant des équations d'Euler-Lagrange (![[*]](crossref.png) ),
multipliant la
),
multipliant la 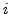 -ième par par
-ième par par 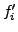 et sommant sur
et sommant sur 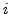 ,
on obtient alors
,
on obtient alors
d'où
On a donc montré

Dans ce cadre aussi, l'absence de dépendance dans la variable
indépendante se traduit par l'existence d'une
quantité conservée.
On verra plus loin une interprétation de cette formule dans le cadre
de la mécanique Hamiltonienne.
Nous avons jusqu'à présent considéré uniquement le cas
de fonctionnelles  dépendant d'une variable dépendante
dépendant d'une variable dépendante 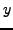 et de sa dérivée
et de sa dérivée 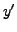 (essentiellement motivés par la formulation
Hamiltonienne de la mécanique classique). On peut en fait étendre
le formalisme du calcul des variations à des cadres plus
larges, comme par exemple le cadre où la fonctionnelle
(essentiellement motivés par la formulation
Hamiltonienne de la mécanique classique). On peut en fait étendre
le formalisme du calcul des variations à des cadres plus
larges, comme par exemple le cadre où la fonctionnelle
 dépend de dérivées d'ordre supérieur de la variable
dépendante
dépend de dérivées d'ordre supérieur de la variable
dépendante 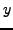 . On est dans ce cas
conduit à des équations différentielles d'ordre supérieur.
. On est dans ce cas
conduit à des équations différentielles d'ordre supérieur.
Par exemple, considérons la fonctionnelle  , définie par
, définie par
et soit 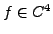 , extrêmum de cette fonctionnelle. Alors, pour
tout
, extrêmum de cette fonctionnelle. Alors, pour
tout 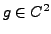 , telle que
, telle que
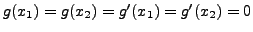 , on a
, on a
Par intégrations par parties successives, et application
du lemme fondamental, on obtient l'équation d'Euler-Lagrange
correspondante
On voit bien que cette équation sera généralement une équation
différentielle d'ordre supérieur.
REMARQUE 1.2 Dans ce cadre, on voit intervenir des dérivées d'ordres supérieurs
des fonctions considérées. Il est donc nécessaire en toute rigueur,
de faire les hypothèses de différentiabilité correspondantes
pour pouvoir énoncer un théorème correct.
Les calculs que nous avons effectués jusqu'à présent
concernaient les situations dans lesquelles les conditions aux bords
sont totalement fixées. Il existe des situations dans lesquelles
les conditions aux bords ne sont pas complètement fixées, et
il est possible d'étendre l'analyse faite plus haut à ces cas de figure.
Prenons par exemple le cas où
![$ f\in C^2([x_1,x_2])$](img239.png) extrêmum
de
extrêmum
de
sous la seule condition aux limites
Dans ce cas, la condition nécessaire d'existence d'un extrêmum
en  s'écrit
s'écrit
pour tout
![$ g\in C^2(]x_1,x_2[)$](img243.png) tel que
tel que 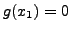 , sans autre condition
en
, sans autre condition
en 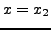 pour
pour 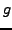 . Ceci implique
. Ceci implique
Ceci étant vérifié pour tout 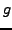 , en particulier pour les
, en particulier pour les 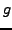 telles que
telles que 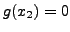 , on en déduit que l'équation
d'Euler-Lagrange (
, on en déduit que l'équation
d'Euler-Lagrange (![[*]](crossref.png) ) reste valide.
De plus, le cas
) reste valide.
De plus, le cas
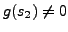 , quelconque, implique
une seconde équation, appelée condition aux bords naturelle
, quelconque, implique
une seconde équation, appelée condition aux bords naturelle
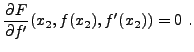 |
(1.11) |
Bruno Torresani
2007-06-26
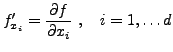
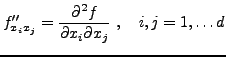
![]() , dont on note
, dont on note
![]() le bord, et
on recherche les extrêma
le bord, et
on recherche les extrêma
![]() de la fonctionnelle
de la fonctionnelle ![]() définie par
définie par
![$\displaystyle \Phi[f] = \int_\Omega F({\underline{x}},f({\underline{x}}),f_{x_1}'({\underline{x}}),f_{x_2}'({\underline{x}}))\, d{\underline{x}}\ .
$](img168.png)
![$\displaystyle D_g\Phi[f] = \left(\frac{d}{d\epsilon} \Phi[f+\epsilon g]\right)_...
...lon=0} =
\lim_{\epsilon\to 0} \frac{\Phi(f+\epsilon g) - \Phi(f)}{\epsilon}\ ,
$](img169.png)
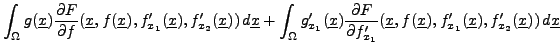
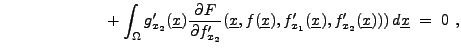

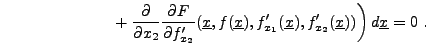
![[*]](crossref.png) ), pour en déduire
), pour en déduire
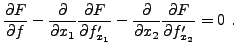
![[*]](crossref.png) .
.
![]() du plan, de bord
du plan, de bord
![]() et la hauteur du film de savon au point
et la hauteur du film de savon au point
![]() est notée
est notée
![]() ,
,
![]() .
L'anneau est modélisé comme une fonction
.
L'anneau est modélisé comme une fonction
![]() , et la surface
du film de savon représenté par
, et la surface
du film de savon représenté par ![]() s'écrit comme
s'écrit comme
![$\displaystyle \Phi[u] = \int_\Omega \sqrt{1 + u'_{x_1}({\underline{x}})^2 + u'_{x_2}({\underline{x}})^2}\,d{\underline{x}}\ .$](img184.png)
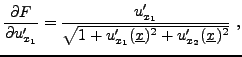
![$\displaystyle \frac{\partial}{\partial x_1}\frac{\partial F}{\partial u'_{x_1}}...
...))}
{[1 + u'_{x_1}({\underline{x}})^2 + u'_{x_2}({\underline{x}})^2]^{3/2}}\ ,
$](img189.png)
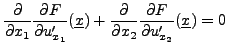
![]() quelconque dans un volume
quelconque dans un volume
![]() est de la forme
est de la forme
![$\displaystyle W[\phi] = \frac{\epsilon_0}2\,\int_\Omega (\nabla\phi({\underline...
...hi'_{x_2}({\underline{x}}),\phi'_{x_3}({\underline{x}})]\,d{\underline{x}}
\ ,
$](img196.png)
![]() par rapport à
par rapport à ![]() , avec conditions
aux bords fixées
, avec conditions
aux bords fixées
![]() sur
sur
![]() , on
obtient l'équation d'Euler-Lagrange
, on
obtient l'équation d'Euler-Lagrange
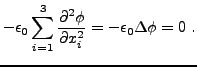
![$\displaystyle I[\phi] = \int_\Omega \left[\left\vert\nabla\phi({\underline{x}},...
...al\phi({\underline{x}},t)}{\partial t}\right)^2\right]\,
d{\underline{x}}dt\ .
$](img203.png)
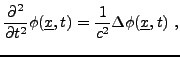
![]() s'écrive sous la forme
s'écrive sous la forme
![$\displaystyle \Phi[f_1,f_2] = \int F(x,f_1(x),f_2(x),f_1'(x),f_2'(x))\,dx\ .
$](img207.png)
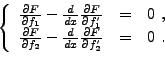

![$\displaystyle {\mathcal A}[q] = \int_{t_1}^{t_2} {\mathcal L}(t,q_1(t),q_2(t),q_3(t),
\dot q_1(t),\dot q_2(t),\dot q_3(t))\, dt\ .
$](img218.png)
![[*]](crossref.png) ) se généralise
elle aussi de façon simple. Supposons que la fonction
) se généralise
elle aussi de façon simple. Supposons que la fonction ![]() ne dépende pas
explicitement de la variable dépendante
ne dépende pas
explicitement de la variable dépendante ![]() , on peut
alors écrire (en omettant les variables, pour simplifier les écritures)
pour tout
, on peut
alors écrire (en omettant les variables, pour simplifier les écritures)
pour tout ![]()
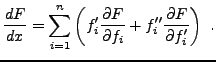
![[*]](crossref.png) ),
multipliant la
),
multipliant la 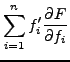
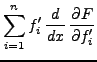
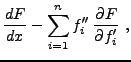
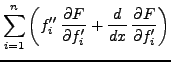
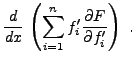

![]() , définie par
, définie par
![$\displaystyle \Phi[f] = \int_{x_1}^{x_2} F(x,f(x),f'(x),f''(x))\,dx\ ,
$](img230.png)
![$\displaystyle \frac{d}{d\epsilon} \Phi[f+\epsilon g]$](img234.png)
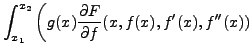

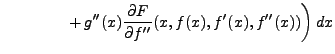
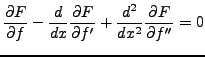
![]() extrêmum
de
extrêmum
de
![$\displaystyle \Phi[f] = \int_{x_1}^{x_2} F(x,f(x),f'(x))\, dx
$](img240.png)
![$\displaystyle \frac{d}{d\epsilon} \Phi[f+\epsilon g]=0
$](img242.png)
![$\displaystyle g(x)\left[\frac{\partial F}{\partial f}(x,f(x),f'(x))
-\frac{d}{dx}\frac{\partial F}{\partial f'}(x,f(x),f'(x))\right]\,dx$](img247.png)
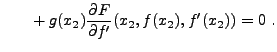
![[*]](crossref.png) ) reste valide.
De plus, le cas
) reste valide.
De plus, le cas