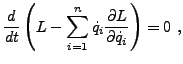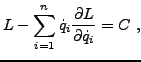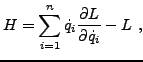Formalisme Hamiltonien
La mécanique Hamiltonienne
est l'exemple le plus classique d'application du calcul variationnel,
et des théorèmes ![[*]](crossref.png) ,
, ![[*]](crossref.png) et
et ![[*]](crossref.png) . Elle postule que la trajectoire
suivie entre les instants
. Elle postule que la trajectoire
suivie entre les instants 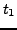 et
et 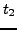 par un système en
mouvement dans l'espace est toujours celle qui optimisera la
quantité suivante, appelée action
par un système en
mouvement dans l'espace est toujours celle qui optimisera la
quantité suivante, appelée action
où 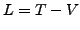 est le Lagrangien, égal à la
différence entre l'énergie cinétique et l'énergie potentielle.
C'est ce que l'on appelle le principe de moindre action
. Le Lagrangien est en fait une
fonctionnelle, qui dépend de la trajectoire suivie.
est le Lagrangien, égal à la
différence entre l'énergie cinétique et l'énergie potentielle.
C'est ce que l'on appelle le principe de moindre action
. Le Lagrangien est en fait une
fonctionnelle, qui dépend de la trajectoire suivie.
Supposons par exemple que le système dynamique considéré soit
décrit par des coordonnées
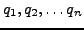 et leurs dérivées
et leurs dérivées
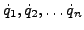 , alors le Lagrangien prend la forme
, alors le Lagrangien prend la forme
et conduit aux équations du mouvement, appelées ici
équations de Lagrange
REMARQUE 1.3 Ces équations du mouvement peuvent aussi être obtenues à partir
des lois de Newton (et sont en fait équivalentes). Toutefois,
pour des systèmes complexes, les équations de Lagrange sont
généralement bien plus faciles à obtenir que ce que l'on pourrait
faire à partir des équations de Newton.
EXEMPLE 1.7 Pendule double:
On considère le pendule double représenté en F
IG. ![[*]](crossref.png)
,
et on note
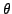
et
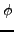
les coordonnées angulaires décrivant les
deux brins.
On choisit pour origine des hauteurs des deux masses leur
hauteur d'équilibre.
L'énergie potentielle est alors donnée par
On montre facilement que l'énergie cinétique est quant à elle
donnée par
Tous calculs faits, les équations d'Euler-Lagrange s'écrivent
Le Hamiltonien:
Supposons maintenant que le Lagrangien ne dépende pas explicitement du
temps. On peut alors utiliser la variante multidimensionnelle
de l'identité de Beltrami (Proposition ![[*]](crossref.png) )
et écrire les équations d'Euler-Lagrange sous la forme
)
et écrire les équations d'Euler-Lagrange sous la forme
ce qui implique que
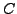 étant une constante. Cette propriété est appelée
loi de conservation. On définit le
Hamiltonien du système par
étant une constante. Cette propriété est appelée
loi de conservation. On définit le
Hamiltonien du système par
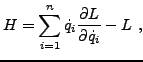 |
(1.12) |
et la loi de conservation stipule donc que le Hamiltonien est une
quantité conservée.
Bruno Torresani
2007-06-26
![[*]](crossref.png) ,
, ![[*]](crossref.png) et
et ![[*]](crossref.png) . Elle postule que la trajectoire
suivie entre les instants
. Elle postule que la trajectoire
suivie entre les instants 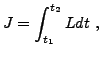
![]() et leurs dérivées
et leurs dérivées
![]() , alors le Lagrangien prend la forme
, alors le Lagrangien prend la forme

![[*]](crossref.png) ,
et on note
,
et on note 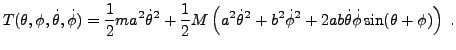
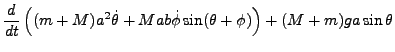
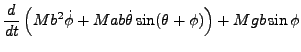
![[*]](crossref.png) )
et écrire les équations d'Euler-Lagrange sous la forme
)
et écrire les équations d'Euler-Lagrange sous la forme