Calcul des variations sous contrainte
Il est parfois possible d'utiliser le même type d'approche pour
résoudre des problèmes variationnels lorsque des contraintes
supplémentaires sont imposées à la solution.
On a alors recours à la méthode des multiplicateurs de Lagrange,
que nous avons déjà vu dans la section ![[*]](crossref.png) , et à une
généralisation du théorème
, et à une
généralisation du théorème ![[*]](crossref.png) .
.
Plus précisément:
![\begin{theorem}
Soit $f: \Omega\subset{\mathbb{R}}^n\to{\mathbb{R}}$, extr\^emum...
...abla f({\underline{x}}))\big]\,d{\underline{x}}-C\ .
\end{equation}\end{theorem}](img267.png)
Notons que 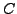 ne joue aucun rôle dans les équations d'Euler-Lagrange
ci-dessus, et peut donc être supprimé. Il doit cependant être pris en
compte (naturellement) lorsque la contrainte est imposée, ce qui
permet de déterminer la valeur du multiplicateur
ne joue aucun rôle dans les équations d'Euler-Lagrange
ci-dessus, et peut donc être supprimé. Il doit cependant être pris en
compte (naturellement) lorsque la contrainte est imposée, ce qui
permet de déterminer la valeur du multiplicateur 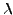 .
.
On peut mettre ce résultat en application sur l'exemple suivant.
EXEMPLE 1.8 Corde pesante à l'équilibre:
on se donne une corde pesante de masse linéique
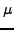
et de
longueur
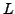
, dans le plan
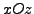
, attachée à ses extrêmités
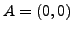
et
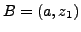
.
La corde est supposée à l'équilibre, donc le problème
se ramène à minimiser l'énergie potentielle
sous la contrainte
On introduit donc la fonctionnelle
à minimiser par rapport à
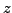
et à
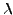
.
Il n'y a pas de dépendance explicite dans la variable indépendante
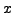
, on peut donc utiliser l'identité de Beltrami, qui s'écrit
et la solution est une chaînette
Les constantes
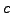
et
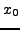
sont déterminées par les conditions
aux limites, et le multiplicateur de Lagrange
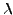
est
quant à lui déterminé en imposant la contrainte.
La physique offre de nombreuses autres applications de ce principe
variationnel sous contrainte. Pour n'en citer qu'un autre, on peut
mentionner que l'équation de Schrödinger.
EXEMPLE 1.9 L'équation de Schrödinger donnant les niveaux
d'énergie d'un opérateur Hamiltonien
où
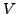
est une fonction à valeurs réelles,
peut être obtenue comme équation d'Euler-Lagrange
d'un problème variationnel (c'est d'ailleurs ainsi que
Schrödinger la formula initialement).
On considère pour cela la fonctionnelle
On montre facilement que la fonction
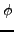
qui minimise cette
fonctionnelle, avec conditions aux limites nulles, et
sous la contrainte de normalisation
doit satisfaire l'équation de Schrödinger ci-dessus.
Bruno Torresani
2007-06-26
![[*]](crossref.png) , et à une
généralisation du théorème
, et à une
généralisation du théorème ![[*]](crossref.png) .
.
![\begin{theorem}
Soit $f: \Omega\subset{\mathbb{R}}^n\to{\mathbb{R}}$, extr\^emum...
...abla f({\underline{x}}))\big]\,d{\underline{x}}-C\ .
\end{equation}\end{theorem}](img267.png)
![]() ne joue aucun rôle dans les équations d'Euler-Lagrange
ci-dessus, et peut donc être supprimé. Il doit cependant être pris en
compte (naturellement) lorsque la contrainte est imposée, ce qui
permet de déterminer la valeur du multiplicateur
ne joue aucun rôle dans les équations d'Euler-Lagrange
ci-dessus, et peut donc être supprimé. Il doit cependant être pris en
compte (naturellement) lorsque la contrainte est imposée, ce qui
permet de déterminer la valeur du multiplicateur ![]() .
.
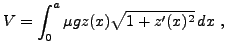
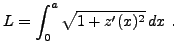
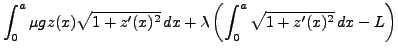
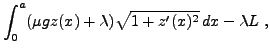
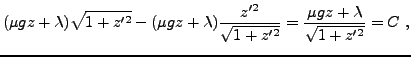
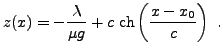
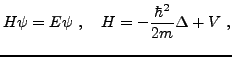
![$\displaystyle \Phi[\psi] = \int_{{\mathbb{R}}^3}\left[\frac{\hbar^2}{2m}\vert\nabla\psi (x)\vert^2
+ V(x)\vert\psi (x)\vert^2\right]\,dx\ .
$](img285.png)