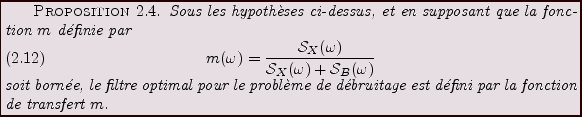Sous-sections
On a souvent recours à des modèles de signaux faisant
intervenir des quantités aléatoires. On peut trouver à
cela deux justifications essentielles:
- La nécessité de modéliser des classes relativement
larges de signaux, regroupés par certaines propriétés
génériques: par exemple, des signaux audiophoniques,
le signal de parole, des images...
- Le besoin de modéliser divers types de ``bruits'' (bruits
de mesure par exemple), généralement difficilement contrôlables.
Le cadre mathématique adapté à cette situation est celui des
processus aléatoires. L'objectif de ce court chapitre est d'aboutir
à la représentation spectrale des processus stationnaires (puis
à la représentation de Karhunen-Loève dans un cadre plus général),
afin d'être en position d'utiliser les outils développés
aux cgapitres précédents.
Dans cette section on désignera par
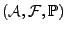 un espace probabilisé. On note par
un espace probabilisé. On note par
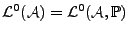 l'espace des variables
aléatoires sur
l'espace des variables
aléatoires sur
 , à valeurs réelles
ou complexes.
Etant données deux variables aléatoires
, à valeurs réelles
ou complexes.
Etant données deux variables aléatoires
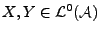 , on dit que
, on dit que 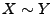 si
si 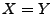 presque surement. Ceci définit une relation
d'équivalence, et on note
presque surement. Ceci définit une relation
d'équivalence, et on note
l'espace quotient, c'est à dire l'espace
des variables aléatoires différentes presque surement.
Etant donnée une variable aléatoire 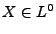 , on en
notera
, on en
notera
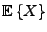 l'espérance.
Un signal aléatoire est en fait un processus stochastique, indexé
par un espace discret ou continu. Plus précisément:
l'espérance.
Un signal aléatoire est en fait un processus stochastique, indexé
par un espace discret ou continu. Plus précisément:
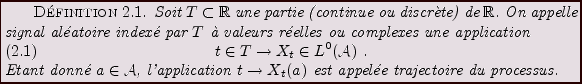
Un sognal aléatoire sera aussi appelé processus aléatoire, processus
stochastique, ou série chronologique. On introduit de même des signaux
aléatoires multidimensionnels (pour lesquels  est une
partie de
est une
partie de
 ), mais on se limitera ici au cas unidimensionnel.
), mais on se limitera ici au cas unidimensionnel.

Un théorème célèbre de Kolmogorov (le théorème d'extension
qui porte son nom) montre que la connaissance du système de lois
marginales est suffisante pour caractériser la distribution du
processus.
Les exemples suivants donnent une idée de la variété des situations
que l'on peut rencontrer.
EXEMPLE 2.1 L'exemple le plus simple est celui d'un bruit blanc discret.
On considère pour cela une famille
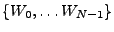
de variables aléatoires indépendantes, identiquement
distribuées, par exemple
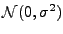
. Il s'agit d'un
processus aléatoire indexé par
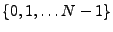
,
que l'on appelle bruit blanc discret Gaussien.
EXEMPLE 2.2 Partant de l'exemple précédent, et étant donnée une suite
finie
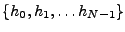
, on peut former la suite
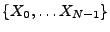
définie par le
produit de convolution circulaire
On a alors par exemple
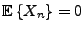
pour tout
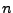
, et aussi
EXEMPLE 2.3 On s'intéressera également à des processus à
temps continu, c'est à dire au cas où
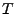
n'est
pas dénombrable. Prenons par exemple
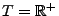
, et
introduisons les temps
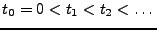
. Soient
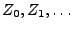
une suite de variables aléatoires sur
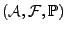
;
on peut alors introduire le processus ``à sauts''

défini par
![$\displaystyle X_t = \sum_{n=0}^\infty Z_n \chi_{[t_n,t_{n+1}]}(t)\ .$](img503.png) |
(2.1) |

est bien un processus aléatoire sur
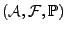
; ses trajectoires
sont des fonctions constantes par morceaux, généralement discontinues
(voir la notion de continuité presque sûre des trajectoires plus bas).
EXEMPLE 2.4 Un processus harmonique est un processus défini sur
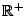
,
de la forme
 |
(2.2) |
où
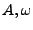
et
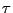
sont des constantes, et où
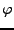
est
une variable aléatoire uniformément distribuée sur
![$ [0,2\pi]$](img509.png)
.

est aussi un processus aléatoire sur
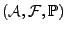
, indexé par
.
Figure:
3 trajectoires de bruit blanc.
|
|
Figure:
3 trajectoires de bruit blanc filtré (filtrage passe-bas).
|
|
En fait, on peut mettre l'accent sur deux classes de processus
particulièrement intéressantes, car basées sur des hypothèses
simplificatrices relativement réalistes dans de nombreux cas pratiques.
- Processus à accroissements indépendants: ce sont les processus tels
que pour tous temps
 , la famille de variables aléatoires
, la famille de variables aléatoires
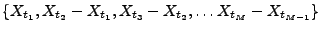 soit une famille de variables aléatoires indépendantes. On verra plus
loin un exemple avec le processus de Wiener.
soit une famille de variables aléatoires indépendantes. On verra plus
loin un exemple avec le processus de Wiener.
- Processus Gaussiens: toutes les mesures de probabilités du
système de lois marginales sont Gaussiennes.
Notons que ces deux hypothèses ne sont pas exclusives
(voir l'exemple du processus de Wiener). L'hypothèse de
``Gaussianité'' est particulièrement utile, car elle permet
de caractériser les distributions de probabilités par leurs
moments d'ordre 1 et 2.
On se limitera dans ce cours au cas des processus du second
ordre c'est à dire des processus tels que leur covariance
est bien définie.

REMARQUE 2.1 Soit
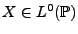
, telle que
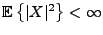
.
Alors il résulte de l'inégalité de Cauchy-Schwarz que
Par conséquent, étant donné un signal aléatoire du second ordre
 , on peut introduire sa moyenne
, on peut introduire sa moyenne
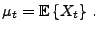 |
(2.3) |
On introduit également la covariance du processus
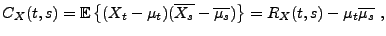 |
(2.4) |
où
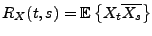 |
(2.5) |
est l'autocorrélation. On a (de nouveau comme conséquence de
l'inégalité de Cauchy-Schwarz), pour tous 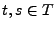
et de même pour 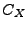 .
Ces deux fonctions vérifient en outre la propriété suivante
.
Ces deux fonctions vérifient en outre la propriété suivante
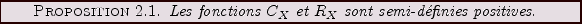
On rappelle qu'une fonction de deux variables 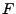 est semi-définie positive
si pour tous
est semi-définie positive
si pour tous
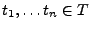 et
et
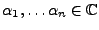 , on a
, on a
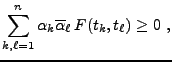 |
(2.6) |
en d'autres termes si la matrice 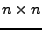
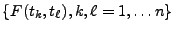 est semi-définie positive pour tous
est semi-définie positive pour tous
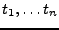 . Elle est définie positive lorsque l'inégalité
est stricte.
. Elle est définie positive lorsque l'inégalité
est stricte.
Preuve de la proposition:
Il suffit de le prouver pour  (la preuve pour
(la preuve pour 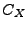 est identique). On a
est identique). On a

Les variables aléatoires  sur
sur
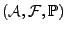 telles que
telles que
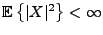 engendrent un espace linéaire, noté
engendrent un espace linéaire, noté
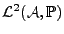 .
Soit
.
Soit
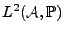 l'espace quotient de
l'espace quotient de
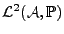 dans lequel on a identifié
les variables aléatoires égales presque sûrement.
dans lequel on a identifié
les variables aléatoires égales presque sûrement.
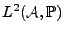 est
naturellement muni d'un produit scalaire défini par
est
naturellement muni d'un produit scalaire défini par
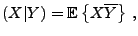 |
(2.7) |
qui en fait un espace de Hilbert.
Etant donné un processus du second ordre
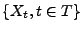 , supposé
centré (c'est à dire tel que
, supposé
centré (c'est à dire tel que
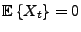 pour tout
pour tout 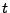 ), on
notera
), on
notera
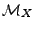 le sous espace fermé de
le sous espace fermé de
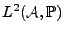 engendré par
les variables aléatoires
engendré par
les variables aléatoires
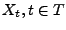 .
.
On se limitera ici au cas des processus du second ordre, indexés par
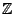 .
Soit donc
.
Soit donc
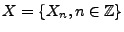 un processus du second ordre sur
un processus du second ordre sur
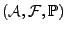 ,
de moyenne
,
de moyenne
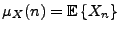 et de fonction de corrélation
et de fonction de corrélation  .
.

Notons que dans ce cas, on a
et de même pour  .
.
On utilise parfois la notion de processus stationnaire au sens
fort (ou strict): de tels processus sont tels que leur distribution
est invariante par translation. De telles hypothèses sont
toutefois souvent trop restrictives, et la stationnarité faible
(c'est à dire en moyenne d'ordre deux) est généralement suffisante.
Les signaux aléatoires du second ordre stationnaires en m.o.d.
restent du second ordre et stationnaires par filtrage numérique.
En effet, soit
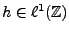 , et soit
, et soit  un signal numérique aléatoire du
second ordre, stationnaire en m.o.d. Soit
un signal numérique aléatoire du
second ordre, stationnaire en m.o.d. Soit 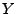 défini par
défini par
Alors 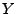 est du second ordre:
est du second ordre:
De plus, on a
et
Ainsi, 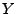 est également stationnaire en moyenne d'ordre deux.
On verra plus loin d'autres exemples de filtrages.
Soit donc
est également stationnaire en moyenne d'ordre deux.
On verra plus loin d'autres exemples de filtrages.
Soit donc  un processus stationnaire en m.o.d.,
que l'on suppose centré pour simplifier. Si tel n'est pas le
cas, on peut toujours écrire
un processus stationnaire en m.o.d.,
que l'on suppose centré pour simplifier. Si tel n'est pas le
cas, on peut toujours écrire 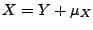 et travailler
sur le signal aléatoire centré
et travailler
sur le signal aléatoire centré 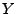 .
En corollaire de ce qui précède, la covariance
.
En corollaire de ce qui précède, la covariance 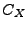 est
une suite définie positive:
pour tous
est
une suite définie positive:
pour tous
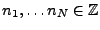 et
et
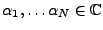 , on a
, on a
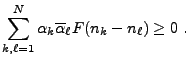 |
(2.8) |
Un résultat général d'analyse fonctionnelle
permet d'introduire la mesure spectrale de  :
:
![\begin{theorem}[Herglotz]
Soit $\phi$\ une suite d\'efinie positive. Alors il ex...
...2\pi}\,\int_{-\pi}^\pi e^{in\omega}\,d\nu(\omega)\ .
\end{equation}\end{theorem}](img552.png)
Preuve:
Commençons par calculer la quantité suivante (qui est
toujours positive ou nulle), pour
![$ \omega\in [-\pi,\pi]$](img553.png)
et posons
Il est clair que
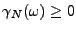 pour tout
pour tout 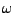 , et que
, et que
Soient 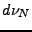 les mesures définies par
les mesures définies par
Il s'agit de mesures bornées, définies sur un domaine compact.
Par conséquent, il est possible d'extraire une sous-suite 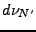 qui converge faiblement vers une limite
qui converge faiblement vers une limite 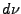 (c'est le théorème
de Helly). De plus, pour tout
(c'est le théorème
de Helly). De plus, pour tout 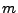 tel que
tel que 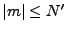 , on a
, on a
Par définition de la convergence faible, on en déduit que
ce qui prouve l'existence de 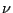 .
.
Pour ce qui est de l'unicité: soient 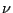 et
et 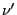 deux limites;
soit
deux limites;
soit
![$ g\in C([-\pi,\pi])$](img567.png) ; on sait que toute fonction
continue est arbitrairement bien
approximée par les polynômes trigonométriques;
; on sait que toute fonction
continue est arbitrairement bien
approximée par les polynômes trigonométriques; 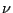 et
et 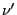 coïncidant sur les polynômes trigonométriques, on a bien
coïncidant sur les polynômes trigonométriques, on a bien
pour tout
![$ g\in C([-\pi,\pi]$](img569.png) , ce qui prouve que
, ce qui prouve que 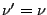 , et donc
l'unicité.
, et donc
l'unicité.

En appliquant ce résultat à la covariance d'un signal aléatoire
du second ordre stationnaire en moyenne d'ordre deux, on
obtient la représentation spectrale suivante (parfois appelée
théorème de Wiener-Khintchin, ou théorème de Wold):
![\begin{corollary}[Wiener-Khintchin]
Soit $X$\ un signal num\'erique al\'eatoire ...
...}\,\int_{-\pi}^\pi e^{in\omega}\,d\nu_X(\omega)\ .
\end{equation}\end{corollary}](img571.png)
La mesure spectrale 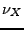 n'est pas nécessairement absolument continue
par rapport à la mesure de Lebesgue. Si c'est le cas, on peut alors
écrire
n'est pas nécessairement absolument continue
par rapport à la mesure de Lebesgue. Si c'est le cas, on peut alors
écrire
où
![$ {\mathcal S}_X\in L^\infty([-\pi,\pi])$](img574.png) est appelé densité spectrale
de
est appelé densité spectrale
de  .
.
- L'exemple le plus simple est celui du bruit blanc Gaussien:
les variables aléatoires
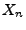 sont des variables aléatoires
Gaussiennes indépendantes et identiquement distribuées
sont des variables aléatoires
Gaussiennes indépendantes et identiquement distribuées
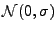 . On a alors
. On a alors 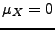 et
et
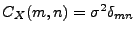 ,
et
,
et  est stationnaire en m.o.d. L'unicité de la mesure spectrale
montre facilement que
est stationnaire en m.o.d. L'unicité de la mesure spectrale
montre facilement que
d'où  admet une densité spectrale
admet une densité spectrale
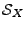 constante.
Ceci explique la terminologie: un bruit blanc est un signal qui
``contient'' toutes les fréquences en égale quantité
(par analogie avec la lumière blanche).
constante.
Ceci explique la terminologie: un bruit blanc est un signal qui
``contient'' toutes les fréquences en égale quantité
(par analogie avec la lumière blanche).
- Bruit blanc filtré (signal MA):
si
 est le bruit blanc précédent, et si
est le bruit blanc précédent, et si
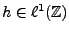 ,
on a déjà vu que
,
on a déjà vu que 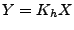 est toujours un processus du second ordre,
stationnaire en m.o.d. Un calcul simple montre que
est toujours un processus du second ordre,
stationnaire en m.o.d. Un calcul simple montre que 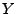 admet une densité
spectrale
admet une densité
spectrale
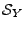 de la forme
de la forme
Plus généralement, si  est un signal aléatoire du second ordre
centré, stationnaire en moyenne d'ordre deux, de densité
spectrale
est un signal aléatoire du second ordre
centré, stationnaire en moyenne d'ordre deux, de densité
spectrale
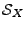 , alors le même calcul montre que
, alors le même calcul montre que 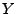 est lui aussi
du second ordre, centré et stationnaire en m.o.d., et tel que
est lui aussi
du second ordre, centré et stationnaire en m.o.d., et tel que
Ainsi, comme dans le cas des signaux déterministes, un
filtrage de convolution revient à ``modeler'' le contenu en fréquences
d'un signal.
- Signal AR: Soit
 un bruit blanc Gaussien comme ci-dessus,
et soient
un bruit blanc Gaussien comme ci-dessus,
et soient
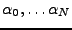 des nombres complexes.
Si il existe un processus
des nombres complexes.
Si il existe un processus 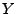 solution de
solution de
alors 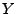 est stationnaire en moyenne d'ordre deux, et admet
une densité spectrale de la forme
est stationnaire en moyenne d'ordre deux, et admet
une densité spectrale de la forme
On verra plus loin une condition suffisante pour l'existence d'un tel 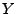 .
.
- Signal ARMA: Soit
 un bruit blanc Gaussien comme ci-dessus,
et soient
un bruit blanc Gaussien comme ci-dessus,
et soient
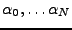 des nombres complexes.
Si il existe un processus
des nombres complexes.
Si il existe un processus 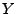 solution de
solution de
alors 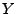 est stationnaire en moyenne d'ordre deux, et admet
une densité spectrale de la forme
est stationnaire en moyenne d'ordre deux, et admet
une densité spectrale de la forme
- Signal harmonique: On considère une variable aléatoire
uniforme
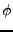 sur l'intervalle
sur l'intervalle
![$ [-\pi,\pi]$](img220.png) (donc, de densité de
probabilités
(donc, de densité de
probabilités
![$ \rho_\phi(\alpha) = \chi_{[-\pi,\pi]}(\alpha)/2\pi$](img590.png) ),
et on lui associe le signal aléatoire
),
et on lui associe le signal aléatoire  défini par
défini par
où
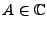 et
et
![$ \omega_0\in [-\pi,\pi]$](img592.png) sont deux constantes.
Il est facile de vérifier que
sont deux constantes.
Il est facile de vérifier que  est du second ordre
(
est du second ordre
(
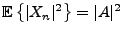 pour tout
pour tout 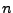 ) et centré. De plus,
) et centré. De plus,
de sorte que  est stationnaire en moyenne d'ordre deux.
Finalement, on a
est stationnaire en moyenne d'ordre deux.
Finalement, on a
d'où on déduit que la mesure spectrale de  n'est autre
que la mesure de Dirac
n'est autre
que la mesure de Dirac
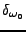 en
en 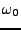 , à un
facteur
, à un
facteur
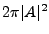 près.
Les signaux harmoniques fournissent l'exemple le plus simple de
signaux aléatoires stationnaires en moyenne d'ordre deux ne possédant
pas de densité spectrale.
près.
Les signaux harmoniques fournissent l'exemple le plus simple de
signaux aléatoires stationnaires en moyenne d'ordre deux ne possédant
pas de densité spectrale.
La théorème de Wiener-Khinchin fournit une
représentation spectrale pour la fonction d'autocovariance
des signaux aléatoires stationnaires en moyenne d'ordre deux.
La question suivante est: pouvons nous obtenir une représentation
similaire (de type ``Fourier'') pour les signaux aléatoires
eux mêmes ?
Nous allons voir dans la section suivante un tel théorème de
représentation spectrale pour les signaux numériques infinis.
Il est utile, pour motiver cette discussion, de faire une parenthèse
avec le cas des signaux numériques aléatoires de longueur finie.
Il est tout d'abord nécessaire d'adapter la définition de stationnarité
à cette situation. Il faut pour cela tenir compte des conditions aux bords,
que l'on suppose ici périodiques.
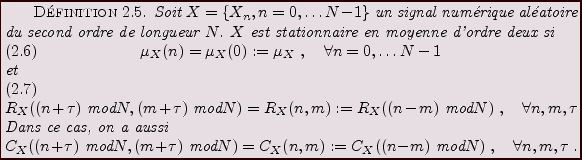
Soit  un tel signal aléatoire, que l'on suppose de plus
centré. Soit
un tel signal aléatoire, que l'on suppose de plus
centré. Soit 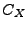 son autocovariance, et soit
son autocovariance, et soit
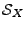 le vecteur
défini par
le vecteur
défini par
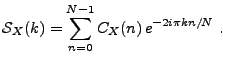 |
(2.9) |
On considère la transformée de Fourier finie de  : le vecteur
aléatoire
: le vecteur
aléatoire
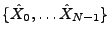 , défini par
, défini par
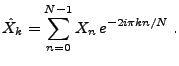 |
(2.10) |
Soit 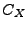 son autocovariance
Un calcul simple montre que
son autocovariance
Un calcul simple montre que
et que
Les composantes de 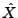 sont donc décorrélées.
Utilisant la transformée de Fourier finie inverse, on peut alors
écrire
sont donc décorrélées.
Utilisant la transformée de Fourier finie inverse, on peut alors
écrire
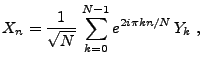 |
(2.11) |
où les variables aléatoires
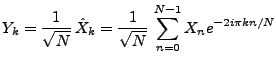 |
(2.12) |
sont décorrélées:
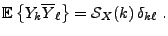 |
(2.13) |
La représentation (![[*]](crossref.png) ) porte parfois le nom de
représentation de Cramèr en dimension finie.
) porte parfois le nom de
représentation de Cramèr en dimension finie.
Application à la simulation numérique de
signaux aléatoires stationnaires:
Lorsque l'on souhaite sinuler numériquement un signal aléatoire,
on se place de facto dans une situation de dimension finie.
Les ordinateurs proposent généralement des générateurs
de nombres pseudo-aléatoires (par exemple, les fonctions de type rand
sour UNIX), capables de fournir des séquences de nombres
aléatoires aussi proches que possible de vecteurs identiquement
distribués et décorrélés. Dans ces conditions, si on
souhaite générer une réalisation d'un signal stationnaire en moyenne
d'ordre deux, de spectre
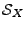 donné, on peut procéder
comme suit: on génère tout d'abord une séquence de nombres
pseudo-aléatoires
donné, on peut procéder
comme suit: on génère tout d'abord une séquence de nombres
pseudo-aléatoires
 , qui sont tels que
, qui sont tels que
puis on exploite la représentation de Cramèr en formant
il est alors facile de vérifier que
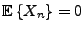 pour tout
pour tout 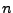 , et que
, et que
ce qui est bien le résultat recherché.
Les sections précédentes nous ont donné une représentation
spectrale (i.e. de type ``Fourier'') pour la covariance d'un
signal numérique aléatoire stationnaire. La covariance est
un objet déterministe. Nous allons maintenant obtenir une
représentation spectrale pour le processus lui même.
On note
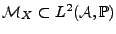 le sous-espace de
le sous-espace de
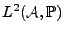 engendré
par les variables aléatoires
engendré
par les variables aléatoires 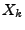 . Soit
. Soit 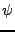 l'application
linéaire de
l'application
linéaire de
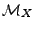 dans
dans
![$ L^2([-\pi,\pi],d\nu_X)$](img615.png) définie par
définie par
Il est clair que
![$ \epsilon_k\in L^2([-\pi,\pi],d\nu_X)$](img617.png) . De plus, on a
. De plus, on a
Ainsi,
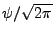 s'étend à une isométrie de
s'étend à une isométrie de
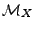 sur
sur
![$ L^2([-\pi,\pi],d\nu_X)$](img615.png) .
Une remarque importante est que
.
Une remarque importante est que
![$ L^2([-\pi,\pi],d\nu_X)$](img615.png) est quant à lui engendré par les fonctions
est quant à lui engendré par les fonctions
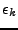 . Ainsi,
l'application
. Ainsi,
l'application
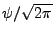 établit une isométrie bijective
établit une isométrie bijective
Soit maintenant
![$ A\subset [-\pi,\pi]$](img622.png) un Borélien, et soit
un Borélien, et soit
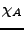 l'indicatrice de
l'indicatrice de 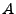 . A
. A 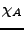 correspond une
variable aléatoire
correspond une
variable aléatoire
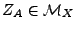 , telle que
, telle que
Ceci s'étend par linéarité aux fonctions simples de la forme
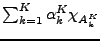 où les
où les 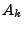 sont des Boréliens
de
sont des Boréliens
de
![$ [-\pi,\pi]$](img220.png) . On a
. On a
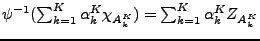 .
Finalement, on sait que toute toute fonction
.
Finalement, on sait que toute toute fonction
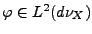 s'écrit comme limite de telles fonctions simples. Le résultat suivant
montre que cette limite a également un sens dans
s'écrit comme limite de telles fonctions simples. Le résultat suivant
montre que cette limite a également un sens dans
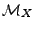 .
.
![\begin{theorem}[Cram\\lq er]
Soit $\varphi\in L^2(d\nu_X)$, et consid\'erons une su...
...equation}et la limite est ind\'ependante de la suite approximante.
\end{theorem}](img630.png)
En appliquant ce résultat au cas particulier
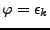 ,
on obtient la représentation spectrale suivante:
,
on obtient la représentation spectrale suivante:
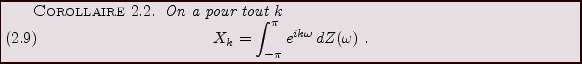
Ce résultat est précisément le résultat auquel on pouvait
s'attendre sur la base de la représentation de Cramèr en dimension
finie: le passage d'un vecteur à une suite infinie oblige à
passer d'un espace de fréquences fini à un espace infini continu
(l'intervalle
![$ [-\pi,\pi]$](img220.png) ).
).
Remarque:
L'objet que l'on a noté
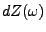 peut être étudié de façon
rigoureuse. Il est utile de noter l'utilisation ``formelle'' qu'en font les
ingénieurs:
peut être étudié de façon
rigoureuse. Il est utile de noter l'utilisation ``formelle'' qu'en font les
ingénieurs:
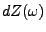 est traité comme une ``mesure aléatoire'',
telle que
est traité comme une ``mesure aléatoire'',
telle que
et
Cette convention de notation permet notamment de retrouver facilement
les propriétés d'isométrie, par exemple, pour toutes
![$ \varphi,\varphi'\in L^2([-\pi,\pi],d\nu_X)$](img636.png) , on écrira formellement
, on écrira formellement
On a vu plus haut l'exemple des filtres de convolution, définis par
une réponse impulsionnelle
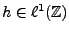 . On voit ici le cas plus
général de filtres définis par leur fonction de transfert.
. On voit ici le cas plus
général de filtres définis par leur fonction de transfert.
Soit 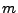 une fonction
une fonction 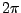 -périodique bornée, que l'on
appellera fonction de transfert. Pour tout un signal numérique
aléatoire du second ordre
-périodique bornée, que l'on
appellera fonction de transfert. Pour tout un signal numérique
aléatoire du second ordre  , centré et stationnaire en
moyenne d'ordre deux, auquel on a associé la mesure
, centré et stationnaire en
moyenne d'ordre deux, auquel on a associé la mesure 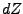 ,
on considère l'application
,
on considère l'application 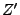 ,
qui à toute fonction
,
qui à toute fonction
![$ \varphi\in L^2([-\pi,\pi],d\nu_X)$](img643.png) associe
associe
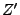 définit un nouveau signal aléatoire
définit un nouveau signal aléatoire 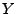 , par
, par
On vérifie facilement que 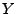 est lui aussi un signal numérique
aléatoire du second ordre, centré, stationnaire en moyenne d'ordre deux,
et de mesure spectrale
est lui aussi un signal numérique
aléatoire du second ordre, centré, stationnaire en moyenne d'ordre deux,
et de mesure spectrale
L'opérateur linéaire 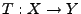 ainsi défini est un
filtre numérique.
L'existence de la représentation spectrale permet de montrer,
sous certaines conditions, l'existence de solutions aux
équations de récursion comme
ainsi défini est un
filtre numérique.
L'existence de la représentation spectrale permet de montrer,
sous certaines conditions, l'existence de solutions aux
équations de récursion comme
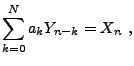 |
(2.14) |
où  est un bruit blanc, et les
est un bruit blanc, et les 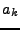 sont des nombres complexes,
sujets à certaines conditions.
sont des nombres complexes,
sujets à certaines conditions.

Preuve: Sous les hypothèses ci-dessus, on note
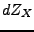 la mesure spectrale de
la mesure spectrale de  .
Pour cela, on considère donc
.
Pour cela, on considère donc 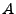 , la transformée en
, la transformée en 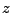 de la suite
de la suite
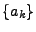 .
. 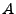 est donc un polynôme de degré
est donc un polynôme de degré 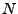 en
en 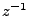 .
Si on suppose que les racines de
.
Si on suppose que les racines de 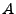 se trouvent à l'intérieur
du disque unité ouvert, la transformée de Fourier discrète
se trouvent à l'intérieur
du disque unité ouvert, la transformée de Fourier discrète
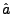 de
de 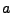 ne s'annulle jamais, de sorte que la fonction
ne s'annulle jamais, de sorte que la fonction
est bornée et donc de carré intégrable; elle admet une série
de Fourier
où la suite
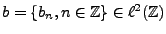 . Le fait que les
racines de
. Le fait que les
racines de 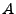 se trouvent toutes à l'intérieur du disque unité implique
que la suite
se trouvent toutes à l'intérieur du disque unité implique
que la suite 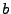 est causale:
est causale:
On considère maintenant le signal aléatoire 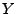 défini par
défini par
On peut alors écrire
de sorte que l'on a bien la propriété requise
On s'intéresse ici à quelques problèmes classiques
de traitement du signal, faisant intervenir des modèles
de signaux aléatoires.
Le problème posé est le suivant: soit
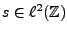 un signal
déterministe, supposé connu, et soit
un signal
déterministe, supposé connu, et soit  un signal aléatoire
du second ordre, centré et stationnaire en m.o.d., admettant une
densité spectrale
un signal aléatoire
du second ordre, centré et stationnaire en m.o.d., admettant une
densité spectrale
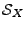 supposée connue elle aussi. On dispose
d'observations de la forme
supposée connue elle aussi. On dispose
d'observations de la forme
et on cherche à construire un filtre numérique 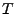 , de fonction
de transfert
, de fonction
de transfert 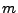 , tel que pour un certain
, tel que pour un certain 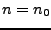 fixé, le rapport
fixé, le rapport
soit maximal. Cette dernière quantité est appelée rapport
signal à bruit, et mesure effectivement l'importance relative du
signal et du bruit en sortie du filtre. Le résultat est donné par
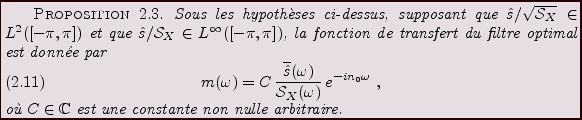
Preuve: partant de
et
on écrit, en utilisant l'inégalité de Cauchy-Schwarz
d'où on déduit la valeur optimale pour le rapport signal à bruit
Finalement, l'inégalité de Cauchy-Schwarz est une égalité
si et seulement si il existe une constante 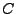 telle que
telle que
qui donne (![[*]](crossref.png) ).
).

On doit en particulier remarquer que
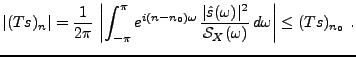 |
(2.15) |
Application:
Le problème de détection se présente généralement
de la façon suivante. On dispose d'observations de la forme
 |
(2.16) |
où
 est un signal déterministe connu,
est un signal déterministe connu,  est
un signal aléatoire du second ordre, centré et stationnaire
en m.o.d., admettant une densité spectrale
est
un signal aléatoire du second ordre, centré et stationnaire
en m.o.d., admettant une densité spectrale
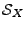 connue elle aussi,
et
connue elle aussi,
et 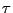 est un décalage temporel inconnu, que l'on cherche
à déterminer.
En appliquant le résultat précédent, dans le cas
est un décalage temporel inconnu, que l'on cherche
à déterminer.
En appliquant le résultat précédent, dans le cas 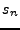 =
=
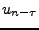 , et
, et 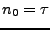 , on obtient un filtre
, on obtient un filtre 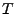 de fonction de transfert
de fonction de transfert
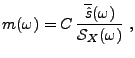 |
(2.17) |
(donc indépendante du paramètre inconnu 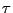 ), tel que
pour tout
), tel que
pour tout 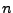
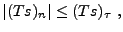 |
(2.18) |
et que la valeur maximale 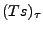 soit la plus grande possible.
L'algorithme de détection consistera à appliquer le filtre
soit la plus grande possible.
L'algorithme de détection consistera à appliquer le filtre 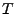 sur le signal observé
sur le signal observé 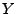 , et à rechercher la valeur
, et à rechercher la valeur 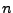 telle que
telle que
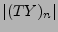 soit la plus grande posible. Ce
soit la plus grande posible. Ce 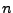 sera alors un candidat
pour le paramètre recherché
sera alors un candidat
pour le paramètre recherché 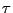 .
.
Pour ce problème, on suppose que l'on dispose d'observations
de la forme
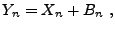 |
(2.19) |
où  et
et 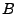 sont deux signaux aléatoires du second ordre,
centrés, stationnaires en m.o.d, possédant des densités
spectrales
sont deux signaux aléatoires du second ordre,
centrés, stationnaires en m.o.d, possédant des densités
spectrales
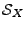 et
et
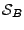 connues:
connues:  est le signal auquel
on s'intéresse, et
est le signal auquel
on s'intéresse, et 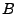 est une perturbation (un bruit) dont on
cherche à se débarrasser. On suppose en outre que
est une perturbation (un bruit) dont on
cherche à se débarrasser. On suppose en outre que  et
et 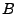 sont
décorrélés:
sont
décorrélés:
On en déduit facilement que 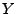 est centré,
stationnaire en moyenne d'ordre deux.
est centré,
stationnaire en moyenne d'ordre deux.
On formule le problème de débruitage de la façon suivante:
trouver un filtre 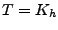 , de réponse impulsionnelle
, de réponse impulsionnelle
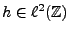 , tel
que
, tel
que 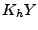 soit aussi proche que possible de
soit aussi proche que possible de  dans le sens suivant:
on souhaite minimiser l'erreur
dans le sens suivant:
on souhaite minimiser l'erreur
 |
(2.20) |
pour tout
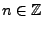 . Il résults de la stationnarité de
. Il résults de la stationnarité de 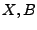 et
et 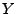 que
que
Le problème peut se formuler dans un cadre Hilbertien. En considérant
l'espace
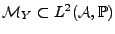 engendré par les variables
aléatoires
engendré par les variables
aléatoires 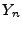 , le problème d'optimisation revient à
rechercher l'élement de
, le problème d'optimisation revient à
rechercher l'élement de
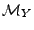 le plus proche de
le plus proche de 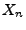 , au sens de la
norme de
, au sens de la
norme de
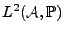 . C'est un problème de projection orthogonale, dont
la solution est caractérisée par les équations
. C'est un problème de projection orthogonale, dont
la solution est caractérisée par les équations
ou encore
En utilisant la décorrélation de  et
et 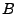 et la stationnarité, on
aboutit au système d'équations suivant:
et la stationnarité, on
aboutit au système d'équations suivant:
Finalement, en utilisant l'expression des fonctions d'autocovariance
à partir des densités spectrales, on aboutit au système d'équations
On obtient ainsi
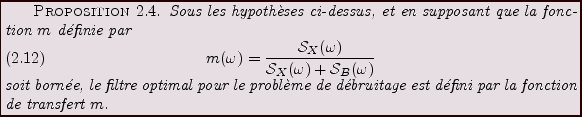
Bruno Torresani
2007-06-26
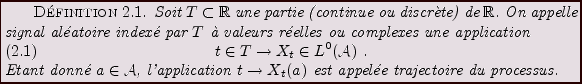

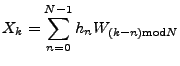
![$\displaystyle X_t = \sum_{n=0}^\infty Z_n \chi_{[t_n,t_{n+1}]}(t)\ .$](img503.png)

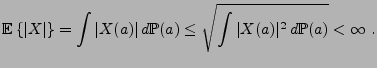
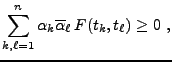
![]() (la preuve pour
(la preuve pour ![]() est identique). On a
est identique). On a
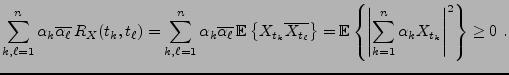
![]() sur
sur
![]() telles que
telles que
![]() engendrent un espace linéaire, noté
engendrent un espace linéaire, noté
![]() .
Soit
.
Soit
![]() l'espace quotient de
l'espace quotient de
![]() dans lequel on a identifié
les variables aléatoires égales presque sûrement.
dans lequel on a identifié
les variables aléatoires égales presque sûrement.
![]() est
naturellement muni d'un produit scalaire défini par
est
naturellement muni d'un produit scalaire défini par

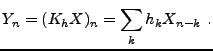
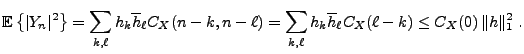
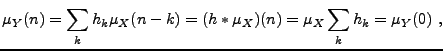
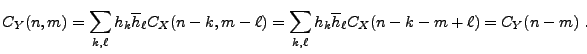
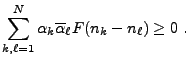
![\begin{theorem}[Herglotz]
Soit $\phi$\ une suite d\'efinie positive. Alors il ex...
...2\pi}\,\int_{-\pi}^\pi e^{in\omega}\,d\nu(\omega)\ .
\end{equation}\end{theorem}](img552.png)
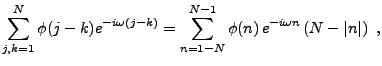
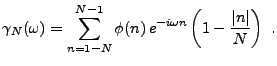
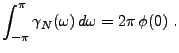
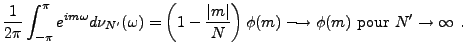
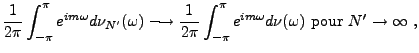
![]() et
et ![]() deux limites;
soit
deux limites;
soit
![]() ; on sait que toute fonction
continue est arbitrairement bien
approximée par les polynômes trigonométriques;
; on sait que toute fonction
continue est arbitrairement bien
approximée par les polynômes trigonométriques; ![]() et
et ![]() coïncidant sur les polynômes trigonométriques, on a bien
coïncidant sur les polynômes trigonométriques, on a bien
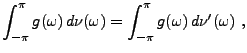
![\begin{corollary}[Wiener-Khintchin]
Soit $X$\ un signal num\'erique al\'eatoire ...
...}\,\int_{-\pi}^\pi e^{in\omega}\,d\nu_X(\omega)\ .
\end{equation}\end{corollary}](img571.png)
![]() n'est pas nécessairement absolument continue
par rapport à la mesure de Lebesgue. Si c'est le cas, on peut alors
écrire
n'est pas nécessairement absolument continue
par rapport à la mesure de Lebesgue. Si c'est le cas, on peut alors
écrire
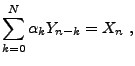

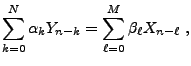
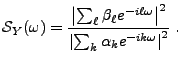
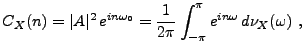
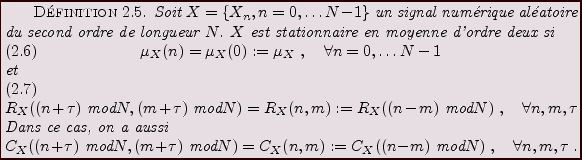
![]() un tel signal aléatoire, que l'on suppose de plus
centré. Soit
un tel signal aléatoire, que l'on suppose de plus
centré. Soit ![]() son autocovariance, et soit
son autocovariance, et soit
![]() le vecteur
défini par
le vecteur
défini par
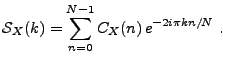
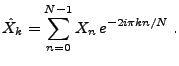
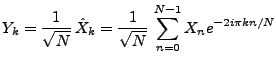
![[*]](crossref.png) ) porte parfois le nom de
représentation de Cramèr en dimension finie.
) porte parfois le nom de
représentation de Cramèr en dimension finie.
![]() donné, on peut procéder
comme suit: on génère tout d'abord une séquence de nombres
pseudo-aléatoires
donné, on peut procéder
comme suit: on génère tout d'abord une séquence de nombres
pseudo-aléatoires
![]() , qui sont tels que
, qui sont tels que
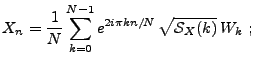
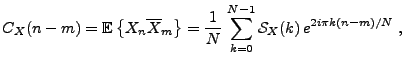
![]() le sous-espace de
le sous-espace de
![]() engendré
par les variables aléatoires
engendré
par les variables aléatoires ![]() . Soit
. Soit ![]() l'application
linéaire de
l'application
linéaire de
![]() dans
dans
![]() définie par
définie par
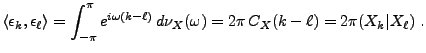
![]() un Borélien, et soit
un Borélien, et soit
![]() l'indicatrice de
l'indicatrice de ![]() . A
. A ![]() correspond une
variable aléatoire
correspond une
variable aléatoire
![]() , telle que
, telle que
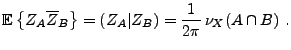
![\begin{theorem}[Cram\\lq er]
Soit $\varphi\in L^2(d\nu_X)$, et consid\'erons une su...
...equation}et la limite est ind\'ependante de la suite approximante.
\end{theorem}](img630.png)
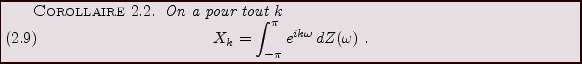
![]() peut être étudié de façon
rigoureuse. Il est utile de noter l'utilisation ``formelle'' qu'en font les
ingénieurs:
peut être étudié de façon
rigoureuse. Il est utile de noter l'utilisation ``formelle'' qu'en font les
ingénieurs:
![]() est traité comme une ``mesure aléatoire'',
telle que
est traité comme une ``mesure aléatoire'',
telle que
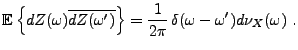
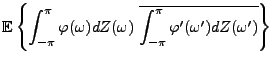
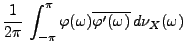
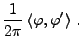
![]() une fonction
une fonction ![]() -périodique bornée, que l'on
appellera fonction de transfert. Pour tout un signal numérique
aléatoire du second ordre
-périodique bornée, que l'on
appellera fonction de transfert. Pour tout un signal numérique
aléatoire du second ordre ![]() , centré et stationnaire en
moyenne d'ordre deux, auquel on a associé la mesure
, centré et stationnaire en
moyenne d'ordre deux, auquel on a associé la mesure ![]() ,
on considère l'application
,
on considère l'application ![]() ,
qui à toute fonction
,
qui à toute fonction
![]() associe
associe
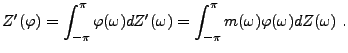
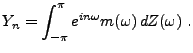

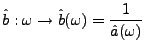
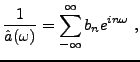
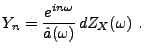
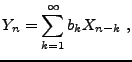
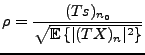
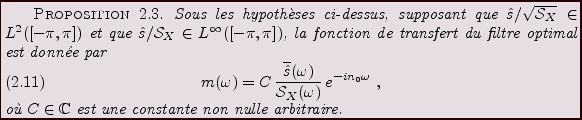
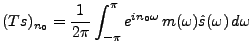
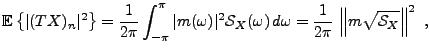
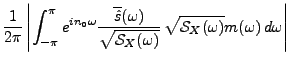
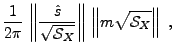
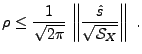

![[*]](crossref.png) ).
).
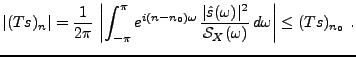
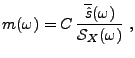
![]() , de réponse impulsionnelle
, de réponse impulsionnelle
![]() , tel
que
, tel
que ![]() soit aussi proche que possible de
soit aussi proche que possible de ![]() dans le sens suivant:
on souhaite minimiser l'erreur
dans le sens suivant:
on souhaite minimiser l'erreur
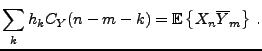
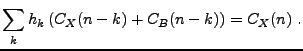
![$\displaystyle \int_{-\pi}^\pi \left[\hat h(\omega) \left({\mathcal S}_X(\omega)...
...ht)
-{\mathcal S}_X(\omega)\right]e^{ik\omega}\,d\omega =0\ ,\quad\forall k\ .
$](img702.png)