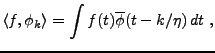Sous-sections
Après avoir analysé les signaux numériques, on passe maintenant
au cas des signaux analogiques. Comme on le verra, toutes les
manipulations que l'on peut effectuer sur les signaux numériques ont leur
contrepartie dans le cas des signaux analogiques, ce dernier cas présentant
quelques difficultés supplémentaires.
On se posera également le problème de l'échantillonnage, c'est à dire
le problème du passage d'un signal analogique à un signal numérique.
Un signal analogique est par définition une fonction d'une
(ou plusieurs) variable(s) continue(s), résultant par exemple
d'une mesure physique. Deux concepts importants sont les concepts
d'énergie et de puissance d'un signal. Pour cela, il est
utile de considérer un exemple.
EXEMPLE 3.1 Considérons un circuit électrique, dont on mesure la
tension aux bornes d'une résistance
. Si on note
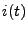
l'intensité du courant dans la résistance,
et
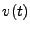
la tension aux bornes de cette dernière,
l'énergie est donnée par
Par conséquent, on appelera par convention énergie
d'un signal le carré de sa norme 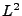
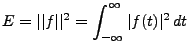 |
(3.1) |
quand celle-ci est définie.
Une autre quantité utile est la puissance d'un signal.
On définit usuellement trois quantités:
- La puissance instantanée:
- La puissance instantanée moyenne
- La puissance moyenne
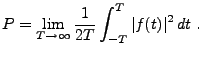 |
(3.2) |
Cette dernière quantité trouve son utilité pour l'étude
des signaux dont l'énergie n'est pas définie.
Un autre ingrédient important de l'analyse du signal
est la théorie spectrale, dont le but est de
simplifier certaines transformations des signaux.
La représentation spectrale des signaux est une représentation
qui fait intervenir des notions fréquentielles plutôt que
des notions temporelles. Pour cela, on doit utiliser
l'analyse de Fourier, ou l'une de ses variantes.
Un cas particulier est fourni par les signaux dits signaux
d'énergie finie, qui ne sont autres que des fonctions de
carré intégrable. La transformation de Fourier
fournit donc un cadre naturel pour construire une théorie
spectrale.
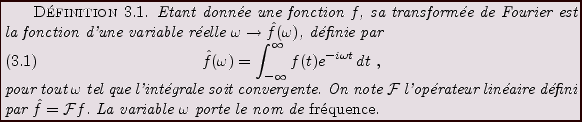
On vérifie immédiatement que si
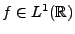 ,
, 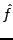 est bornée.
Plus généralement, on a
est bornée.
Plus généralement, on a
![\begin{theorem}[Riemann-Lebesgue]
Soit $f\in L^1({\mathbb{R}})$. Alors $\hat f$\...
...h}
\lim_{\omega\to\pm\infty}\hat f(\omega) = 0\ .
\end{displaymath}\end{theorem}](img715.png)
Preuve:
Nous savons déjà que si
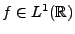 , alors
, alors 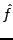 est bornée.
Passons à la continuité.
La preuve est relativement simple. Commençons par calculer
est bornée.
Passons à la continuité.
La preuve est relativement simple. Commençons par calculer
Le fait que  soit intégrable implique qu'il existe
soit intégrable implique qu'il existe 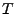 tel que
tel que
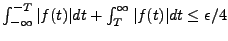 .
Nous n'avons donc plus qu'à nous préoccuper de l'intégrale
entre
.
Nous n'avons donc plus qu'à nous préoccuper de l'intégrale
entre 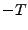 et
et 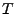 . Mais dans cet intervalle, nous savons que
. Mais dans cet intervalle, nous savons que
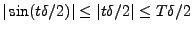 . Donc, nous avons
. Donc, nous avons
Il suffit maintenant de choisir 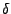 de sorte que
de sorte que
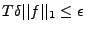 , et on obtient bien
l'estimation souhaitée (
, et on obtient bien
l'estimation souhaitée (![[*]](crossref.png) ).
La première partie du théorème est donc montrée.
).
La première partie du théorème est donc montrée.
Le fait que
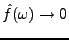 quand
quand
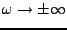 résulte de la densité des fonctions constantes par morceaux
dans l'espace
résulte de la densité des fonctions constantes par morceaux
dans l'espace
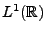 : pour toute fonction
: pour toute fonction
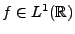 , il existe
une suite de fonctions
, il existe
une suite de fonctions  , constantes par morceaux, telle que
pour tout
, constantes par morceaux, telle que
pour tout 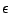 fixé, on ait
fixé, on ait
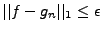 pour
un
pour
un 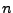 assez grand. Il suffit donc d'étudier le comportement
de la fonction caractéristique d'un intervalle; prenons
assez grand. Il suffit donc d'étudier le comportement
de la fonction caractéristique d'un intervalle; prenons
![$ g=\chi_{[a,b]}$](img732.png) . Alors, on a
. Alors, on a
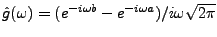 , qui tend bien vers 0 quand
, qui tend bien vers 0 quand
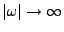 .
De même, la transformée de Fourier de toute fonction intégrable
constante par morceaux tend vers 0 à l'infini. Pour conclure, il
suffit de remarquer que pour tout
.
De même, la transformée de Fourier de toute fonction intégrable
constante par morceaux tend vers 0 à l'infini. Pour conclure, il
suffit de remarquer que pour tout 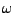 , on a par hypothèse
, on a par hypothèse
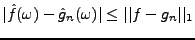 . Comme pour tout
. Comme pour tout 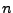 ,
,
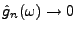 quand
quand
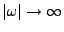 , et comme
, et comme
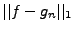 peut
être rendu aussi prôche de 0 que ce que l'on veut, on en déduit
que
peut
être rendu aussi prôche de 0 que ce que l'on veut, on en déduit
que
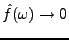 quand
quand
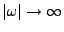 .
.

La transformation de Fourier possède des propriétés simples, faciles
à vérifier. En supposant que
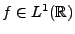 pour simplifier (ce qui
assure l'existence de
pour simplifier (ce qui
assure l'existence de
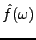 pour tout
pour tout 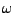 , on
vérifie facilement les propriétés suivantes:
, on
vérifie facilement les propriétés suivantes:
- Comportement vis à vis des translations et des modulations.
Considérons maintenant une fonction intégrable
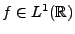 .
On définit la translatée de
.
On définit la translatée de  par la quantité
par la quantité
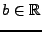 comme la fonction
comme la fonction
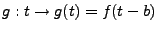 .
On a alors, par un simple changement de variables
.
On a alors, par un simple changement de variables
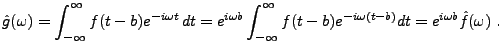 |
(3.3) |
On dit que 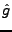 est une version modulée de
est une version modulée de
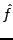 . Similairement, si
. Similairement, si
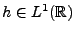 , définie par
, définie par
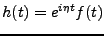 (où
(où
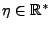 ) est une version
modulée de la fonction intégrable
) est une version
modulée de la fonction intégrable  , alors on a
, alors on a
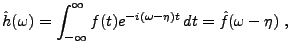 |
(3.4) |
de sorte que la transformée de Fourier de 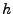 est une version
translatée de
est une version
translatée de 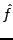 .
.
- Comportement vis à vis des dilatations.
Soit
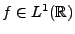 , et soit
, et soit 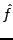 sa
transformée de Fourier. Si
sa
transformée de Fourier. Si 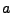 est une constante réelle,
on considère une fonction
est une constante réelle,
on considère une fonction 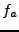 , dilatée de
, dilatée de  du
facteur
du
facteur 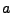 , définie par
, définie par
Alors, on a, par un changement de variable 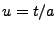 ,
,
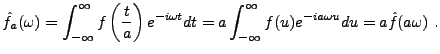 |
(3.5) |
Ainsi, la transformée de Fourier de la copie dilatée d'une fonction
n'est autre qu'une copie dilatée (d'un rapport inverse) de la
transformée de Fourier de la fonction originale.
Le problème de l'inversion de la transformation de Fourier
est un délicat problème. La transformation de Fourier
inverse est définie par:
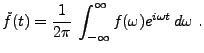
et on note
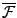 l'opérateur linéaire défini par
l'opérateur linéaire défini par
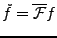 .
Le problème qui se pose est de donner un sens à
.
Le problème qui se pose est de donner un sens à 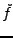 ,
mais aussi de définir dans quelles conditions
et en quel sens
,
mais aussi de définir dans quelles conditions
et en quel sens
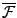 est effectivement la transformation
inverse de la transformation de Fourier
est effectivement la transformation
inverse de la transformation de Fourier
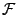 .
.
Le résultat suivant, appelé formule d'échange, joue
un rôle essentiel dans ce qui suit.
![\begin{lemma}[Formule d'\'echange]
Soient $f,g\in L^1({\mathbb{R}})$. Alors on a...
...ion}
\int f(t)\hat g(t) dt = \int \hat f(s) g(s) ds\ .
\end{equation}\end{lemma}](img756.png)
Preuve: la preuve est une conséquence immédiate
du théorème de Fubini.

Ce résultat permet d'obtenir la première version de la
formule d'inversion:
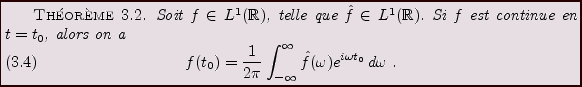
Preuve:
Considérons la famille de fonctions intégrables
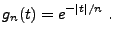 |
(3.6) |
Leur transformée de Fourier est donnée par
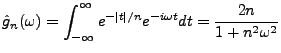 |
(3.7) |
La formule d'échange donne alors
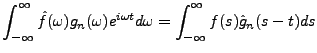 |
(3.8) |
Intéressons nous tout d'abord au terme de gauche de cette égalité.
Nous savons que
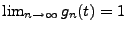 pour tout
pour tout  , et que
par ailleurs,
, et que
par ailleurs,
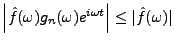 , qui est borné.
Le théorème de convergence dominée
de Lebesgue nous assure donc que pour tout
, qui est borné.
Le théorème de convergence dominée
de Lebesgue nous assure donc que pour tout 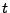 ,
,
Passons maintenant au membre de droite, et notons tout d'abord que
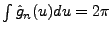 . Calculons
. Calculons
![$\displaystyle \int_{-\infty}^\infty f(s+t) \hat g_n(s) ds -2\pi f(t) = \int_{-\infty}^\infty \left[f(s+t)-f(t)\right]\hat g_n(s) ds \ .$](img765.png) |
(3.9) |
Supposons que  soit continue en
soit continue en 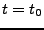 . Donc, pour tout
. Donc, pour tout
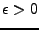 , il existe un
, il existe un 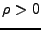 tel que
tel que 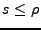 entraîne
entraîne
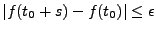 . En traitant de façon différente
les valeurs
. En traitant de façon différente
les valeurs 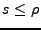 et
et 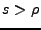 dans le membre de droite
de (
dans le membre de droite
de (![[*]](crossref.png) ), nous sommes amenés à considérer
), nous sommes amenés à considérer
que nous pouvons rendre aussi petit que nous voulons. Quant à l'autre
terme, nous avons à considérer
qui tend vers zéro quand
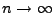 , et
, et
qui tend lui aussi vers zéro quand
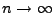 . Ainsi, la limite du
membre de droite de (
. Ainsi, la limite du
membre de droite de (![[*]](crossref.png) ), au point de continuité
), au point de continuité 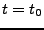 ,
n'est autre que
,
n'est autre que 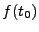 . Ceci achève la preuve du théorème.
. Ceci achève la preuve du théorème.

Il est possible de montrer des résultats plus généraux. On citera
par exemple le résultat suivant, donné sans démonstration.

Nous allons maintenant nous focaliser quelque peu sur les
propriétés de régularité des transformées de
Fourier des fonctions intégrables. La continuité est
réglée par le théorème de Riemann-Lebesgue.
Le cas de la dérivabilité de la transformée de Fourier se traite
de façon similaire, et fait apparaitre la relation entre dérivation
de 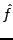 et multiplication par
et multiplication par 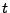 de
de 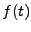 . Supposons que
. Supposons que
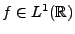 , et que de plus la fonction
, et que de plus la fonction
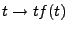 appartienne elle aussi
à
appartienne elle aussi
à
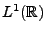 . Comme dans la preuve du théorème de Riemann-Lebesgue, on a
. Comme dans la preuve du théorème de Riemann-Lebesgue, on a
On peut alors diviser les deux membres de cette équation
par 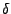 , et utiliser des estimations similaires à celles
utilisées dans la preuve du théorème de Riemann-Lebesgue,
pour montrer que la limite quand
, et utiliser des estimations similaires à celles
utilisées dans la preuve du théorème de Riemann-Lebesgue,
pour montrer que la limite quand
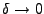 existe, et est
précisément égale à la transformée de Fourier de
existe, et est
précisément égale à la transformée de Fourier de
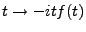 . On a donc, sous les hypothèses faites,
. On a donc, sous les hypothèses faites,
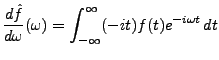 |
(3.10) |
ce qui revient à dériver sous le signe somme.
En utilisant ce résultat de façon récursive, on obtient

On se pose maintenant la question ``duale'', à savoir,
``quelle est la transformée de la dérivée d'une fonction ?''
Nous allons montrer le résultat suivant:
 = (i\omega)^k \hat f(\omega)\ .
\end{equation}\end{proposition}](img783.png)
Preuve:
Pour démontrer ce résultat, considérons une fonction  satisfaisant aux hypothèses du théorème, et remarquons tout
d'abord que comme
satisfaisant aux hypothèses du théorème, et remarquons tout
d'abord que comme 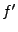 est supposée intégrable, on a
est supposée intégrable, on a
et dont
 existe.
existe.  étant intégrable, cette
limite est nécessairement nulle. De même, on a
étant intégrable, cette
limite est nécessairement nulle. De même, on a
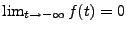 . On peut donc intégrer par parties dans
l' intégrale qui définit la transformée de Fourier de
. On peut donc intégrer par parties dans
l' intégrale qui définit la transformée de Fourier de 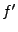 ,
et on obtient
,
et on obtient
et donc
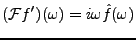 |
(3.11) |
De façon plus générale, en intégrant par parties autant de fois
qu'il le faut, on obtient de même, pour 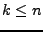 ,
,
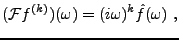 |
(3.12) |
ce qui est le résultat souhaité.

REMARQUE 3.1 Ce dernier résultat nous donne un critère simple pour vérifier
si la transformée de Fourier
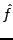
d'une fonction
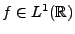
est elle
même intégrable, et donc de lui appliquer la version ponctuelle de la
formule d'inversion. En effet, si on suppose
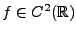
, et
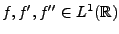
, alors il en résulte que
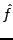
est bornée, et
décroît au moins aussi bien que
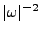
à l'infini.
Dans ce cas, on a donc bien
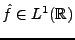
.
REMARQUE 3.2 La P
ROPOSITION ![[*]](crossref.png)
fournit un exemple d'un comportement
général de la transformation de Fourier:
plus une fonction est
régulière, plus sa transformée de Fourier est rapidement décroissante.
Dans le cas particulier, si toutes les dérivées de

jusqu'à
l'ordre
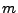
sont dans
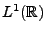
(ce qui est une forme de régularité),
alors comme
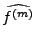
est bornée (par Riemann-Lebesgue),
ceci implique que
pour une certaine constante positive
(rappelons que
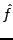
est
également bornée). Il est possible de démontrer des
résultats similaires en supposant d'autres formes de régularité.
L'espace
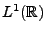 ne donne pas un cadre suffisant pour la théorie
de Fourier, et le cadre le plus naturel est
ne donne pas un cadre suffisant pour la théorie
de Fourier, et le cadre le plus naturel est
 3.1. Cependant, la définition de la transformation de Fourier
dans
3.1. Cependant, la définition de la transformation de Fourier
dans
 n'est pas facile (pour une fonction
n'est pas facile (pour une fonction
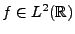 ,
,
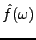 n'est pas nécessairement défini pour tout
n'est pas nécessairement défini pour tout 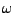 ).
).
Il est nécessaire, pour construire la théorie de Fourier
sur
 , d'employer des moyens détournés, à savoir des arguments
de densité.
Commençons par considérer l'espace des fonctions
, d'employer des moyens détournés, à savoir des arguments
de densité.
Commençons par considérer l'espace des fonctions  à support borné
à support borné
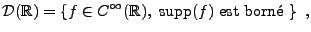 |
(3.13) |
Il est aussi utile d'introduire la notion de fonction à
décroissance rapide.
![\begin{definition}[Fonction \\lq a d\'ecroissance rapide]
Soit $f$\ une fonction co...
...n}
\vert f(t)\vert \le \frac{C_k}{\vert t\vert^k}
\end{equation}\end{definition}](img802.png)
Il s'agit donc de fonctions qui décroissent à l'infini plus vite que
toutes les puissances. Ceci nous permet d'introduire l'espace de
Schwartz
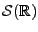 (parfois appelé aussi classe de Schwartz):
(parfois appelé aussi classe de Schwartz):
 |
(3.14) |
On a des relations d'inclusion simples
 |
(3.15) |
Deux remarques sont importantes à faire.
Tout d'abord, il est facile de voir que
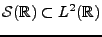 |
(3.16) |
En effet, si
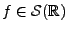 , nous savons qu'il existe une constante
, nous savons qu'il existe une constante 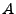 telle
que
telle
que
Par conséquent,
ce qui montre que
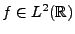 .
.
Le second point important est contenu dans la proposition suivante:

Un corollaire immédiat est que
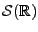 est lui aussi dense
dans
est lui aussi dense
dans
 . C'est sur cette propriété que nous allons nous
appuyer pour étendre la transformation de Fourier à
. C'est sur cette propriété que nous allons nous
appuyer pour étendre la transformation de Fourier à
 .
.
L'espace de Schwartz
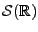 possède une propriété remarquable:
la transformée de Fourier d'une fonction appartenant à
possède une propriété remarquable:
la transformée de Fourier d'une fonction appartenant à
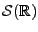 est
elle aussi une fonction de
est
elle aussi une fonction de
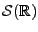 . Pour nous en convaincre,
commençons par faire les remarques suivantes:
. Pour nous en convaincre,
commençons par faire les remarques suivantes:
- Si
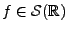 , alors pour tout polynôme
, alors pour tout polynôme 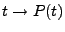 , la
fonction
, la
fonction
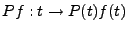 est elle aussi une fonction de
est elle aussi une fonction de
 .
.
- Si
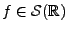 , alors
, alors
 , et plus généralement,
toutes les dérivées
, et plus généralement,
toutes les dérivées 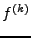 de
de  sont des fonctions de
sont des fonctions de
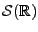 .
.
-
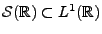 .
.
On déduit de ces remarques que la transformation de Fourier est bien
définie sur
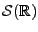 : toute fonction de
: toute fonction de
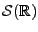 possède une
transformée de Fourier bornée.
De plus, si
possède une
transformée de Fourier bornée.
De plus, si
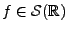 , alors pour tout
, alors pour tout 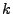 ,
,
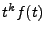 est aussi dans
est aussi dans
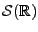 et est ainsi intégrable; donc
et est ainsi intégrable; donc
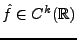 , et ce pour tout
, et ce pour tout 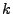 . Donc
. Donc
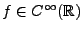 .
Le même raisonnement s'applique à toutes les dérivées de
.
Le même raisonnement s'applique à toutes les dérivées de  :
:
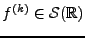 implique que la fonction
implique que la fonction
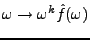 est bornée, et ce quel que
soit
est bornée, et ce quel que
soit 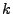 . Donc nous avons montré que la transformée de Fourier
. Donc nous avons montré que la transformée de Fourier
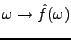 de toute fonction
de toute fonction
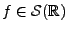 est elle même
une fonction de
est elle même
une fonction de
 .
.
Inversement,
 , et la discussion
précédente s'applique tout aussi bien à
, et la discussion
précédente s'applique tout aussi bien à 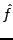 . Par conséquent,
nous avons montré
. Par conséquent,
nous avons montré

Soient
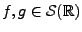 , et posons
, et posons
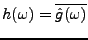 .
Alors un calcul simple montre que
.
Alors un calcul simple montre que
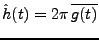 .
Appliquons la formule d'échange à
.
Appliquons la formule d'échange à  et
et 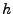 . Ceci nous donne la
formule de Plancherel:
. Ceci nous donne la
formule de Plancherel:
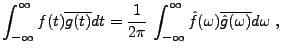 |
(3.17) |
et en particulier dans le cas 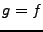 :
:
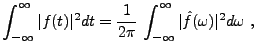 |
(3.18) |
(il découle de la discussion ci-dessus que toutes ces intégrales
sont convergentes. Par conséquent, dans ce cas, nous avons aussi
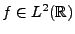 et
et
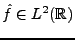 .)
Nous avons donc montré:
.)
Nous avons donc montré:

Le passage au cadre
 se fait en utilisant la densité de
se fait en utilisant la densité de
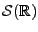 dans
dans
 , et le théorème général d'analyse fonctionnelle
suivant:
, et le théorème général d'analyse fonctionnelle
suivant:

En considérant le cas
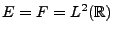 et
et
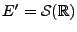 ,
,
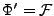 (la transformation de Fourier sur
(la transformation de Fourier sur
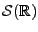 ), et en utilisant les
résultats obtenus dans la sous-section précédente, on
obtient directement le résultat important suivant:
), et en utilisant les
résultats obtenus dans la sous-section précédente, on
obtient directement le résultat important suivant:
![\begin{theorem}[Transformation de Fourier sur $L^2({\mathbb{R}})$]
La transforma...
...y \hat f(\omega) \overline{\hat g(\omega)}d\omega\ .
\end{equation}\end{theorem}](img837.png)
REMARQUE 3.3 Il est facile de vérifier que la formule d'échange reste valable
dans le cadre

.
Ce dernier résultat, pour important qu'il soit, n'est pas
constructif, au sens où la transformation de Fourier dans
 n'y est construite que par un argument de passage à la limite abstrait.
Il est complété par la proposition suivante, qui prouve que la
transformée de Fourier d'une fonction de
n'y est construite que par un argument de passage à la limite abstrait.
Il est complété par la proposition suivante, qui prouve que la
transformée de Fourier d'une fonction de
 s'obtient (aux points oú
elle est bien définie) via le calcul usuel.
s'obtient (aux points oú
elle est bien définie) via le calcul usuel.
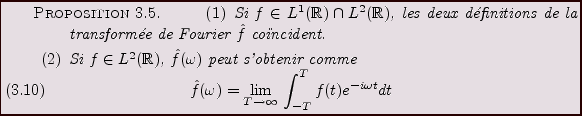
Preuve:
1) Notons temporairement 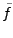 la transformée de Fourier de
la transformée de Fourier de  au sens
au sens
 . Etant donnée
. Etant donnée
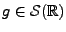 , on a d'après la formule
d'échange (voir Remarque
, on a d'après la formule
d'échange (voir Remarque ![[*]](crossref.png) )
)
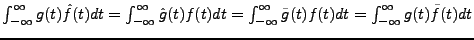 .
Par conséquent,
.
Par conséquent,
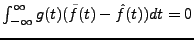 pour tout
pour tout
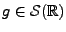 , et donc
, et donc
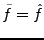 presque partout.
presque partout.
2) Il suffit de remarquer que pour toute fonction
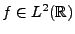 , on peut
écrire
, on peut
écrire
c'est à dire que
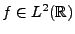 est arbitrairement bien approximée par
des fonctions
est arbitrairement bien approximée par
des fonctions
![$ f\chi_{[-T,T]}$](img845.png) , pour
, pour 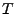 assez grand. Or ces dernières
appartiennent à
assez grand. Or ces dernières
appartiennent à
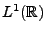 , donc leur transformée de Fourier est bien
définie. D'après la formule de Plancherel, on a ainsi
, donc leur transformée de Fourier est bien
définie. D'après la formule de Plancherel, on a ainsi
![$ \lim_{T\to\infty}\Vert\hat f-\widehat{f\chi_{[-T,T]}}\Vert =
\lim_{T\to\infty}\Vert f-f\chi_{[-T,T]}\Vert = 0$](img846.png) , ce qui conclut la
preuve de la proposition.
, ce qui conclut la
preuve de la proposition.

EXEMPLE 3.2 Considérons la fonction

définie par
Cette fonction n'est pas intégrable, mais elle appartient à

.
Sa transformée de Fourier est facilement obtenue grâce à la
méthode des résidus, et on obtient
où
est la fonction de Heaviside.
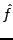
est bien
de carré intégrable, mais est discontinue.
Un ingrédient crucial de la théorie
 tient à l'impossibilité
de localiser parfaitement une fonction simultanément dans l'espace
tient à l'impossibilité
de localiser parfaitement une fonction simultanément dans l'espace
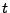 et dans l'espace de Fourier. Ceci est exprimé par
les Inégalités de Heisenberg formulées pour la première fois
par W. Heisenberg, et prouvées en 1927 par N. Wiener:
et dans l'espace de Fourier. Ceci est exprimé par
les Inégalités de Heisenberg formulées pour la première fois
par W. Heisenberg, et prouvées en 1927 par N. Wiener:
![\begin{theorem}[Heisenberg-Wiener]
Soit $f\in L^2({\mathbb{R}})$, $f\ne 0$. On p...
...{displaymath}
f(t) = a e^{ib t} e^{-(t-c)^2/d}\ .
\end{displaymath}\end{theorem}](img850.png)
Preuve:
On peut sans perte de généralité supposer que les quantités
considérées sont finies (sinon l'inégalité est trivialement satisfaite).
Dans ces conditions, le fait que
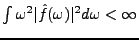 implique que
implique que  est continue et
est continue et
 .
Supposons tout d'abord que
.
Supposons tout d'abord que
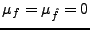 .
Par intégration par parties, on a
.
Par intégration par parties, on a
Comme
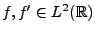 , de même que la fonction
, de même que la fonction
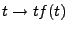 , les intégrales
ci-dessus ont une limite lorsque
, les intégrales
ci-dessus ont une limite lorsque
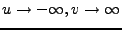 , de même que
, de même que
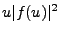 et
et 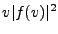 . De plus, ces dernières limites sont nécessairement
nulles, sinon on aurait
. De plus, ces dernières limites sont nécessairement
nulles, sinon on aurait
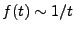 quand
quand
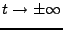 , ce qui est
incompatible avec
, ce qui est
incompatible avec
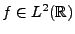 .
.
Donc, en prenant la valeur absolue
et en développant la dérivée, on a
En appliquant l'inégalité de Cauchy-Schwarz à ces deux termes,
on aboutit à
Or, nous savons que la transformée de Fourier de 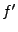 n'est autre
que la fonction
n'est autre
que la fonction
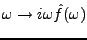 .
En utilisant la formule de Plancherel, nous obtenons
.
En utilisant la formule de Plancherel, nous obtenons
On a bien le résultat désiré, dans le cas
particulier
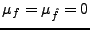
Pour le cas général, considérons la fonction 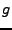 définie par
définie par
Un calcul immédiat montre que
 ,
de sorte que l'on peut appliquer à
,
de sorte que l'on peut appliquer à 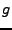 le résultat
que nous venons de montrer. Or, on a
le résultat
que nous venons de montrer. Or, on a
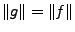 ,
,
et
Ceci conclut la démonstration.

Ces inégalités nous montrent que l'on ne peut pas espérer
trouver de fonction qui soit parfaitement localisée simultanément
en temps et en fréquence. Une autre question que l'on peut se
poser est une version un peu plus faible: peut on trouver
des fonctions à support compact, dont la transformée de
Fourier soit elle aussi à support compact ?
Le résultat suivant apporte une réponse négative à cette question.
![\begin{proposition}[Paley-Wiener]
Soit $f\in L^2({\mathbb{R}})$\ une fonction no...
...pport compact, alors $f$\ ne
peut s'annuler sur un intervalle.
\end{proposition}](img870.png)
Preuve: Il suffit de démontrer la seconde assertion,
la première s'en déduit immédiatement. Supposons donc que
le support de 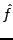 soit inclus dans
soit inclus dans ![$ [-b,b]$](img871.png) , et que pour
tout
, et que pour
tout
![$ t\in [c,d]$](img872.png) , on ait
, on ait 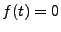 . Soit
. Soit 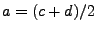 . On sait que
. On sait que
(où l'égalité est ponctuelle: puisque
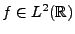 , alors
, alors
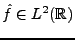 ; de plus, comme le support de
; de plus, comme le support de 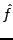 est borné,
alors
est borné,
alors
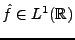 , ce qui donne une fonction
, ce qui donne une fonction  continue).
Compte tenu des hypothèses faites sur
continue).
Compte tenu des hypothèses faites sur  dans
dans ![$ [c,d]$](img876.png) , on sait que
pour tout entier positif ou nul
, on sait que
pour tout entier positif ou nul 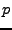 , on a
, on a
En développant
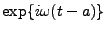 en série entière,
on a aussi pour tout
en série entière,
on a aussi pour tout 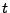
ce qui contredit l'hypothèse 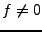 .
.

Etant données deux fonctions  et
et 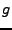 , leur produit
de convolution est la fonction définie par
, leur produit
de convolution est la fonction définie par
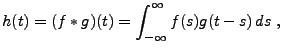 |
(3.19) |
pour tout 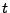 tel que l'intégrale ait un sens. On vérifie
immédiatement que si
tel que l'intégrale ait un sens. On vérifie
immédiatement que si
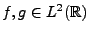 ,
, 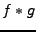 est une fonction
bornée. De plus, elle est continue.
est une fonction
bornée. De plus, elle est continue.
Plus généralement, on a les inégalités de Young:
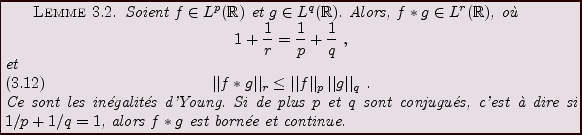
REMARQUE 3.4 On voit en particulier que tous les espaces
sont
stables par convolution avec les fonctions de
: si
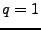
,
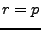
.
Un cas qui nous intéressera plus particulièrement est le cas
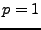
,
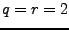
.
La transformation de Fourier associe de façon étroite
le produit de convolution au produit simple. Formellement, on a
Le problème est de donner un sens à ces égalités.
On peut en particulier considérer les situations suivantes:
- Si
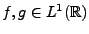 , alors on sait d'après les inégalités
d'Young que
, alors on sait d'après les inégalités
d'Young que
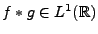 , et donc que la transformée de
Fourier de
, et donc que la transformée de
Fourier de 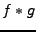 est bornée et continue. De même,
est bornée et continue. De même, 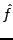 et
et 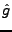 sont bornées et continues. L'égalité (
sont bornées et continues. L'égalité (![[*]](crossref.png) ) est
donc valable point par point.
) est
donc valable point par point.
- Si
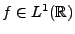 et
et
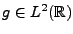 : alors,
: alors,
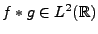 , de même
que
, de même
que
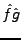 . L'égalité, valable au sens de
. L'égalité, valable au sens de
 ,
se montre en utilisant un argument de densité. Soit
,
se montre en utilisant un argument de densité. Soit
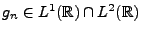 une suite telle que
une suite telle que 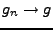 dans
dans
 . D'après ce qui précède,
on sait que
. D'après ce qui précède,
on sait que
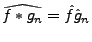 point par point. De plus,
la continuité de la transformation de Fourier implique que
point par point. De plus,
la continuité de la transformation de Fourier implique que
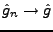 , et
, et
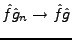 , ce qui permet
de conclure.
, ce qui permet
de conclure.
- Passons à (
![[*]](crossref.png) ), et considérons le cas simple
), et considérons le cas simple
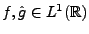 . On peut alors définir
. On peut alors définir 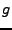 par transformation de
Fourier inverse, et
par transformation de
Fourier inverse, et
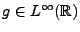 . On a alors
. On a alors
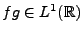 ,
et
,
et
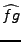 est bornée et continue. De même,
est bornée et continue. De même,
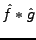 est continue et bornée. Le théorème de Fubini
s'applique, et l'égalité est valable point par point.
est continue et bornée. Le théorème de Fubini
s'applique, et l'égalité est valable point par point.
- Si on suppose maintenant
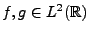 . Alors,
. Alors,
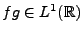 , et on a
de nouveau égalité point par point.
, et on a
de nouveau égalité point par point.
- Il est encore possible de donner un sens à ces égalités
dans des cas plus généraux, mais il faut travailler plus.
Etant donnée
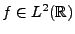 , on définit sa
fonction d'autocorrélation
, on définit sa
fonction d'autocorrélation
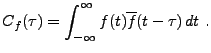 |
(3.22) |
On vérifie immédiatement que
De plus, 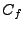 est une fonction continue.
est une fonction continue.
Etant donnée
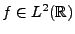 , considérons la fonction définie par
, considérons la fonction définie par
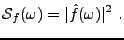 |
(3.23) |
Cette fonction est appelée spectre , ou densité spectrale
de  .
.
Comme
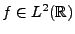 ,
,
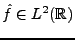 , et
, et
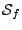 est intégrable.
Donc, sa transformée de Fourier inverse a un sens, et définit une
fonction bornée continue. Ainsi, on a
est intégrable.
Donc, sa transformée de Fourier inverse a un sens, et définit une
fonction bornée continue. Ainsi, on a
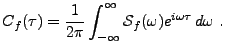 |
(3.24) |
C'est le théorème de Wiener-Khintchin (ou théorème de Wold). On a
en particulier, pour 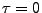
Le spectre
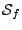 possède une interprétation physique importante.
La valeur
possède une interprétation physique importante.
La valeur
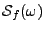 caractérise le ``contenu'' du signal
caractérise le ``contenu'' du signal  à la fréquence
à la fréquence 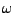 . L'énergie
. L'énergie 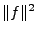 de
de  est la
somme des valeurs de la densité spectrale à toutes les fréquences.
C'est pourquoi on parle également de spectre d'énergie, ou de
densité spectrale d'énergie.
La théorie de Wiener a pour but d'étendre la théorie
précédente au cas des signaux d'énergie non bornée.
Dans ce cas, l'énergie n'étant pas définie,
il est nécessaire de raisonner en termes de puissance. La théorie
spectrale de Wiener permet d'obtenir une version adaptée à ce nouveau
contexte du théorème de Wiener-Khintchin (
est la
somme des valeurs de la densité spectrale à toutes les fréquences.
C'est pourquoi on parle également de spectre d'énergie, ou de
densité spectrale d'énergie.
La théorie de Wiener a pour but d'étendre la théorie
précédente au cas des signaux d'énergie non bornée.
Dans ce cas, l'énergie n'étant pas définie,
il est nécessaire de raisonner en termes de puissance. La théorie
spectrale de Wiener permet d'obtenir une version adaptée à ce nouveau
contexte du théorème de Wiener-Khintchin (![[*]](crossref.png) ).
).
Soit
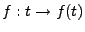 une fonction, telle que
une fonction, telle que
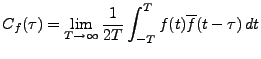 |
(3.25) |
existe et est fini
 .
. 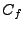 est appelée
autocovariance de
est appelée
autocovariance de  , et
, et
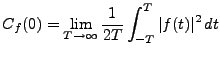 |
(3.26) |
est la puissance totale de  .
.
On considère l'espace de Besicovitch (ou espace des fonctions quasi périodiques)
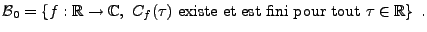 |
(3.27) |
L'application
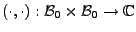 définie par
définie par
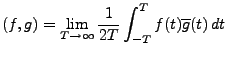 |
(3.28) |
munit
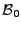 d'un produit scalaire indéfini, c'est à dire
vérifie les quatre premières propriétés de la
définition
d'un produit scalaire indéfini, c'est à dire
vérifie les quatre premières propriétés de la
définition ![[*]](crossref.png) .
.
REMARQUE 3.5
En particulier, toutes les fonctions de carré intégrable
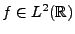 sont telles que
sont telles que 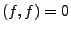 .
.
Cependant, les propriétés essentielles sont préservées.
En particulier, l'inégalité de Cauchy-Schwarz est préservée:
si
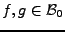 , on a
, on a
d'où on déduit, par passage à la limite
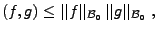 |
(3.29) |
où on a posé, pour
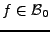 ,
,
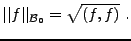 |
(3.30) |
On en déduit en particulier
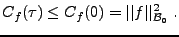 |
(3.31) |
REMARQUE 3.6 Les fonctions
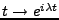
, où
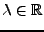
, appartiennent à
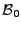
. Elles forment même un système orthonormé dans
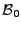
.
La fonction d'autocovariance possède la propriété
fondamentale suivante

Preuve: il suffit d'écrire
et le résultat en découle.

On est alors en position d'utiliser le résultat
classique suivant
![\begin{theorem}[Bochner]
Soit $F$\ une fonction d\'efinie non-n\'egative,
contin...
...\int_{-\infty}^\infty e^{i\omega t} d\nu (\omega)\ .
\end{equation}\end{theorem}](img939.png)
Considérons une décomposition de Lebesgue de la mesure 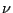 :
:
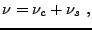 |
(3.32) |
où 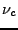 est absolument continue par rapport à la mesure de
Lebesgue, et
est absolument continue par rapport à la mesure de
Lebesgue, et 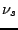 est singulière. Considérons tout d'abord des
cas séparés:
Ainsi, dans le cas des signaux de puissance finie (et non plus d'énergie
finie), on peut encore obtenir une représentation spectrale, et
introduire une notion de densité spectrale adaptée. Cette théorie est
à la base de la théorie spectrale de Wiener pour les signaux aléatoires.
est singulière. Considérons tout d'abord des
cas séparés:
Ainsi, dans le cas des signaux de puissance finie (et non plus d'énergie
finie), on peut encore obtenir une représentation spectrale, et
introduire une notion de densité spectrale adaptée. Cette théorie est
à la base de la théorie spectrale de Wiener pour les signaux aléatoires.
Le filtrage est généralement considéré comme l'opération
de base du traitement du signal. Le filtrage (linéaire) est
utilisé pour résoudre de nombreux problèmes, allant de
la modification de signaux (pour le codage par modulation
d'amplitude ou de fréquence) à l'identification de paramètres
en passant par le débruitage.
On se limitera ici au problème du filtrage linéaire. Comme on
va le voir, un filtre linéaire est souvent un opérateur de convolution.
C'est en particulier le cas des filtres analogiques qui peuvent être
implémentés par des circuits électriques. Cependant ça n'est pas le
cas le plus général, et on verra des contre-exemples simples.
On se posera alors le problème classique de synthèse de filtres:
étant donné un filtre 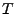 , comment l'approximer par un filtre
réalisable par un circuit électronique.
, comment l'approximer par un filtre
réalisable par un circuit électronique.
Les traiteurs de signaux utilisent volontiers une terminologie quelque
peu différente de la terminologie mathématique classique. En
particulier:
- Système: Un système est une transformation qui associe
à un signal d'énergie finie un autre signal d'énergie finie.
C'est l'analogue d'un opérateur borné sur
 .
.
- Système linéaire: opérateur linéaire borné sur
 .
.
- Filtre linéaire: opérateur linéaire qui commute
avec les translations.
Cette dernière contrainte signifie que le filtre
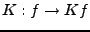 est tel que si on définit
est tel que si on définit 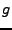 par
par
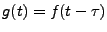 , on a
, on a
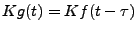 .
.
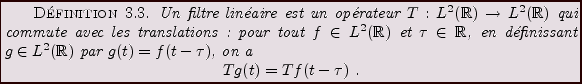
Les exemples les plus simples de filtres linéaires sont les
opérateurs de convolution. Soit
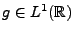 , et soit
, et soit 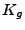 l'opérateur défini par
l'opérateur défini par
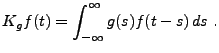 |
(3.34) |
Il est immédiat que 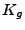 est borné, et que c'est un filtre
linéaire. On a aussi
est borné, et que c'est un filtre
linéaire. On a aussi
de sorte qu'un filtrage de convolution se ramène à un produit
simple dans l'espace de Fourier.
Plus généralement, on a le résultat suivant, que nous donnons sans
démonstration:
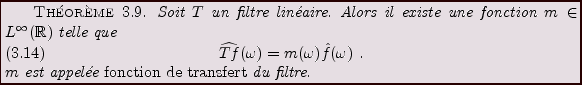
REMARQUE 3.7 Il est immédiat que l'on a
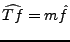
, et donc, en introduisant
le
spectre d'énergie,
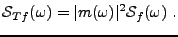 |
(3.35) |
On dit que le filtrage modifie le contenu fréquentiel du signal. Par exemple,
si
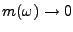
quand
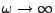
, la décroissance à l'infini de
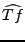
est plus rapide que celle de
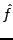
, et l'on s'attend donc
à ce que
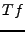
soit une fonction plus ``régulière'' que

. Nous verrons
des conséquences importantes de cette remarque plus loin.
On considère souvent des filtres linéaires de la forme 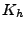 ,
où
,
où
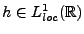 .
.

La contrainte de causalité est importante quand il s'agit de donner une
implémentation ``physique'' du filtre (par un circuit électrique par exemple).
En effet, si 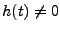 sur un ensemble de mesure non-nulle de
sur un ensemble de mesure non-nulle de
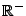 , le calcul de
, le calcul de
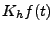 pour un temps
pour un temps 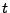 donné
donné
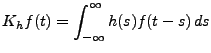
utilise des valeurs 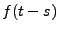 antérieures à
antérieures à 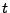 , ce qui est irréalisable.
, ce qui est irréalisable.
- Le filtre passe-bas idéal: étant donnée une fréquence
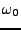 (appelée fréquence de coupure), le filtre passe-bas
idéal est défini par
(appelée fréquence de coupure), le filtre passe-bas
idéal est défini par
Il est immédiat de montrer que la réponse impulsionnelle
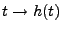 du filtre est de la forme
du filtre est de la forme
Donc,
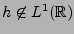 , et le filtre n'est pas stable. Il n'est pas
réalisable non plus de façon évidente.
, et le filtre n'est pas stable. Il n'est pas
réalisable non plus de façon évidente.
- Le filtre passe-haut idéal: étant donnée une fréquence de coupure
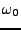 , le filtre passe-haut
idéal est défini par
, le filtre passe-haut
idéal est défini par
On vérifie immédiatement qu'il n'est ni stable ni réalisable.
- On définit également des filtres passe-bande
(définis par
![$ m(\omega) =\chi_{[a,b]}(\omega)$](img982.png) ) et des filtres
coupe-bande (définis par
) et des filtres
coupe-bande (définis par
![$ m(\omega) =1-\chi_{[a,b]}(\omega)$](img983.png) ),
qui ne sont eux aussi ni stables ni réalisables.
),
qui ne sont eux aussi ni stables ni réalisables.
Une façon simple de construire des filtres réalisables
est d'utiliser des circuits électriques. Par exemple, un circuit
du type de celui de la Fig. ![[*]](crossref.png) .
.
Figure:
Le filtre 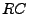
|
|
En notant
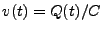 la tension aux bornes du condensateur, la loi
d'Ohm s'écrit
la tension aux bornes du condensateur, la loi
d'Ohm s'écrit
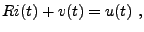 |
(3.36) |
ce qui entraîne, puisque
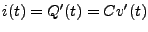 , que la tension
, que la tension
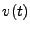 satisfait à l'équation différentielle ordinaire
satisfait à l'équation différentielle ordinaire
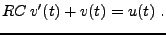 |
(3.37) |
Pour résoudre cette dernière, il est utile d'introduire la fonction
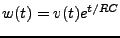 . On a donc
. On a donc
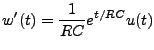 |
(3.38) |
et la solution est
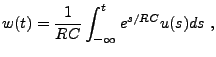 |
(3.39) |
soit
où nous avons posé
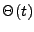 étant la fonction d'Heaviside, qui vaut 1 pour
étant la fonction d'Heaviside, qui vaut 1 pour 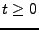 et 0 pour
et 0 pour 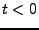 . Nous sommes bien en présence d'un filtre réalisable
et stable.
. Nous sommes bien en présence d'un filtre réalisable
et stable.
Plus généralement, on peut à partir de circuits analogiques obtenir
des systèmes linéaires dont l'entrée 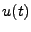 et la sortie
et la sortie 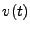 sont liés par une équation différentielle du type
sont liés par une équation différentielle du type
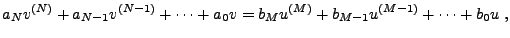 |
(3.42) |
complétée par des conditions initiales adéquates.
Un calcul immédiat montre que la fonction de transfert correspondante
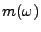 est donnée par
est donnée par
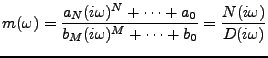 |
(3.43) |
Pour que la fonction de transfert soit bornée, on a nécessairement
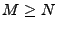 . Il faut également que le dénominateur soit
borné inférieurement (en module) par une constante strictement
positive. Comme on le voit, la variable
. Il faut également que le dénominateur soit
borné inférieurement (en module) par une constante strictement
positive. Comme on le voit, la variable 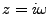 s'introduit
naturellement3.2.
s'introduit
naturellement3.2.
Le résultat suivant donne une première caractérisation
de la structure des filtres réalisables que l'on peut espérer
obtenir à base de circuits analogiques.

Preuve: Notons 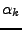 les racines (complexes) de
les racines (complexes) de 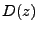 , et
soit
, et
soit 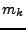 leur multiplicité:
leur multiplicité:
En décomposant 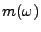 en éléments simples, on aboutit
à une forme
en éléments simples, on aboutit
à une forme
où 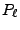 est un polynôme de degré inférieur à
est un polynôme de degré inférieur à 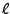 .
.
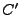 est une constante, qui correspond à un multiple de l'identité.
On supposera dans la suite que
est une constante, qui correspond à un multiple de l'identité.
On supposera dans la suite que 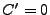 (ce qui est le cas dès que
(ce qui est le cas dès que 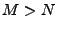 ).
).
Soit
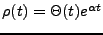 , où
, où
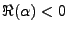 .
Un calcul immédiat donne
.
Un calcul immédiat donne
 .
Plus généralement, si
.
Plus généralement, si
on a
Donc, la transformée de Fourier inverse de
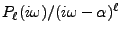 est
est
Par conséquent, si
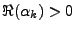 pour tout
pour tout 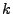 , la
réponse impulsionnelle du filtre est de la forme
, la
réponse impulsionnelle du filtre est de la forme
où les 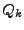 sont des polynômes. Il s'agit bien de filtres
stables et réalisables.
sont des polynômes. Il s'agit bien de filtres
stables et réalisables.
Inversement, supposons que pour une certaine racine 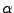 de
de 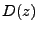 , on ait
, on ait
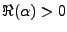 . Un calcul similaire au précédent
montre que la transformée de Fourier inverse de
. Un calcul similaire au précédent
montre que la transformée de Fourier inverse de
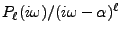 est proportionnelle
à
est proportionnelle
à
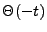 , ce qui est incompatible avec la causalité.
Ceci achève la preuve de la proposition.
, ce qui est incompatible avec la causalité.
Ceci achève la preuve de la proposition.

On s'intéresse souvent au problème de construire des filtres
à partir d'une réponse attendue sur le spectre du signal.
Plus précisément, on recherche à construire un filtre de
fonction de transfert 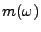 telle que
telle que
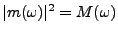 ,
où
,
où 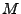 est une fonction donnée, paire à valeurs réelles
positives.
est une fonction donnée, paire à valeurs réelles
positives.
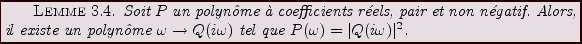
Preuve: Soit
 une racine de
une racine de  . D'après la
parité de
. D'après la
parité de 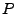 ,
, 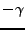 est également racine de
est également racine de 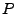 . Si
. Si 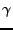 est
complexe,
est
complexe,
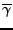 et
et
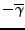 sont également
racines. Si
sont également
racines. Si
 et
et
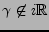 ,
,
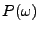 contient nécessairement un terme de la forme
contient nécessairement un terme de la forme
avec
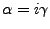 . Ce terme a bien la forme annoncée.
. Ce terme a bien la forme annoncée.
Si
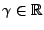 , alors
, alors 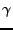 est nécessairement
de multiplicité paire: en effet,
est nécessairement
de multiplicité paire: en effet, 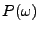 contient obligatoirement
un terme en
contient obligatoirement
un terme en
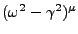 ,
, 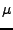 étant la multiplicité
de
étant la multiplicité
de 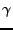 , et pour que
, et pour que 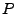 soit positif
soit positif 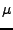 doit nécessairement
être pair. Donc
doit nécessairement
être pair. Donc
avec
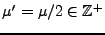 et toujours
et toujours
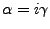 ,
est lui aussi de la forme annoncée.
,
est lui aussi de la forme annoncée.
Si
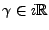 ,
, 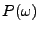 contient nécessairement
un terme en
contient nécessairement
un terme en
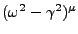 , qui est toujours positif,
et de la forme
, qui est toujours positif,
et de la forme
Il suffit alors d'utiliser la factorisation de  pour obtenir le résultat.
pour obtenir le résultat.

REMARQUE 3.8 Si nécessaire, il est possible de construire le polynôme
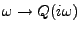
en n'utilisant que les racines
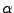
de partie réelle négative, et les racines imaginaires pures
avec la moitié de leur multiplicité.
On peut maintenant passer au cas des filtres rationnels. Soit donc
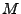 une fonction rationnelle de
une fonction rationnelle de 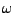 , de la forme
, de la forme
On peut alors appliquer le traitement précédent à 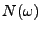 et
et
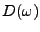 , et on obtient:
, et on obtient:

Preuve:
It suffit d'utiliser le lemme précédent. Le dénominateur
nécessite un traitement particulier, afin d'assurer la
causalité du filtre. Cependant, la REMARQUE ![[*]](crossref.png) montre qu'il est possible de se limiter dans ce cas à des racines
de partie réelle négative (le fait que la fraction rationnelle
considérée soit bornée implique que le dénominateur n'a aucune
racine imaginaire pure).
montre qu'il est possible de se limiter dans ce cas à des racines
de partie réelle négative (le fait que la fraction rationnelle
considérée soit bornée implique que le dénominateur n'a aucune
racine imaginaire pure).

Figure:
Fonctions de transfert des filtres de Butterworth (à gauche)
et Chebyshev (à droite) d'ordres 5 (trait plein), 10 (tirets) et
20 (tirets et pointgillés).
|
|
EXEMPLE 3.3 Les deux familles classiques d'exemples de filtres rationnels
approchant des filtres idéaux sont fournies par les filtres
de Butterworth et les filtres de Chebyshev. On se limite ici
au cas des filtres passe-bas.
Les filtres de Butterworth sont les plus simples, et sont
donnés par une fonction de transfert de la forme
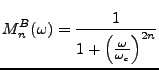 |
(3.44) |
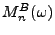
approche la fonction de transfert (en module carré)
d'un filtre passe-bas idéal, de fréquence de coupure
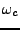
.
Les pôles correspondants sont égaux aux racines
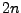
-ièmes
de
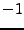
, multipliées par
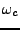
. L'avantage des filtres de
Butterworth est que la fonction
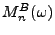
est ``plate'' en
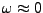
. Plus précisément, elle se comporte comme
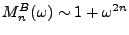
pour
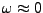
.
Une alternative est fournie par les filtres de Chebyshev, définis
à partir des polynômes de Chebyshev
par
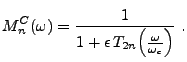 |
(3.45) |
Le paramètre
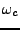
contrôle la largeur du filtre.
Les filtres de Chebyshev présentent quant à eux l'avantage d'être
mieux localisés (plus ``étroits''), mais ceci se fait au
prix d'oscillations apparaissant pour
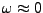
.
L'amplitude des oscillations est gouvernée par le paramètre
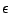
.
On se pose maintenant le problème ``pratique'' suivant.
Comment construire un système linéaire 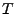 (plus précisément,
un filtre linéaire) dont la réponse
(plus précisément,
un filtre linéaire) dont la réponse 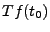 en
en 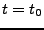 soit maximale
quand une entrée donnée
soit maximale
quand une entrée donnée  lui est présentée ?
Le cadre naturel pour ce problème est le cadre des signaux aléatoires.
Cependant, on peut développer une première approche dans le cadre
déterministe (l'aléatoire étant généralement invoqué pour
traiter les bruits de mesure).
Plus précisément, soit
lui est présentée ?
Le cadre naturel pour ce problème est le cadre des signaux aléatoires.
Cependant, on peut développer une première approche dans le cadre
déterministe (l'aléatoire étant généralement invoqué pour
traiter les bruits de mesure).
Plus précisément, soit
 , et soit
, et soit  un filtre linéaire.
On sait donc que
un filtre linéaire.
On sait donc que
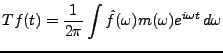
pour une certaine fonction
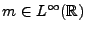 . Pour s'affranchir de la
normalisation de
. Pour s'affranchir de la
normalisation de 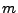 , il faut introduire une contrainte.
On cherche à résoudre le problème
, il faut introduire une contrainte.
On cherche à résoudre le problème
 |
(3.46) |
Plus généralement, soit 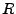 une fonction réelle telle
que
une fonction réelle telle
que
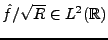 et
et
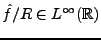 .
Ces conditions sont vérifiées dès que
.
Ces conditions sont vérifiées dès que
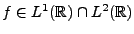 et qu'il existe deux constantes positives
et qu'il existe deux constantes positives
 et
et  telles que pour tout
telles que pour tout 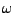 ,
,
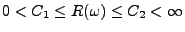 ,
mais ceci n'est pas une condition nécessaire.
On s'intéresse alors au problème
,
mais ceci n'est pas une condition nécessaire.
On s'intéresse alors au problème
 |
(3.47) |
REMARQUE 3.9 On suppose implicitement que
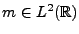
, ce qui permet d'assurer
que
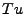
est bornée pour tout
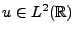
.
Dans un cas comme dans l'autre, la réponse est contenue dans
l'inégalité de Cauchy-Schwarz: il suffit d'écrire
D'autre part, l'égalité est atteinte si et seulement si
pour une certaine constante 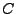 .
En tenant compte de la normalisation, on aboutit ainsi à la
solution suivante
.
En tenant compte de la normalisation, on aboutit ainsi à la
solution suivante
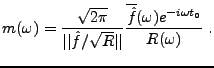 |
(3.48) |
Les hypothèses faites assurent que
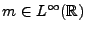 , et on a ainsi
, et on a ainsi
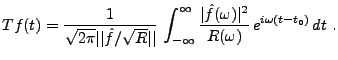 |
(3.49) |
l'opérateur 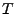 ainsi défini est un filtre, et on a pour tout
ainsi défini est un filtre, et on a pour tout 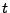 ,
,
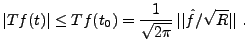 |
(3.50) |
Notons que dans le cas particulier 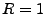 , on a
, on a
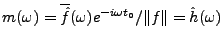 ,
avec
,
avec
 .
.
On a donc montré

REMARQUE 3.10 Notons que si
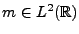
, c'est à dire si
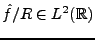
,
le filtre adapté
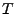
est continu de

sur
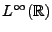
,
ce qui est une propriété importante d'un point de vue pratique.
Ce résultat a des conséquences pratiques importantes.
Considérons le problème de détection suivant:
supposons connu un signal de référence 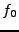 , et
supposons que l'on dispose d'observations de la forme
, et
supposons que l'on dispose d'observations de la forme
où 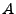 et
et 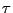 sont deux paramètres inconnus,
sont deux paramètres inconnus,
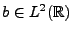 représente
un bruit de mesure dont seul le spectre d'énergie
représente
un bruit de mesure dont seul le spectre d'énergie
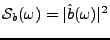 est connu. Le problème de détection
optimale consiste à déterminer les valeurs des paramètres
est connu. Le problème de détection
optimale consiste à déterminer les valeurs des paramètres
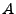 et
et 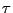 à partir de l'observation.
à partir de l'observation.
Considérons tout d'abord le cas 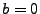 . On commence alors
par construire un système linéaire
. On commence alors
par construire un système linéaire 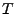 tel que
tel que
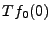 soit le plus grand possible. La solution nous est donnée
par la théorie ci-dessus:
soit le plus grand possible. La solution nous est donnée
par la théorie ci-dessus: 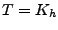 , où
, où 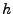 est définie par
est définie par
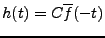 . On sait de plus que pour tout
. On sait de plus que pour tout 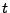 ,
,
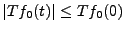 .
Alors, compte tenu du fait que le filtre
.
Alors, compte tenu du fait que le filtre 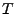 est linéaire et
commute avec les translations, on sait que
est linéaire et
commute avec les translations, on sait que
et 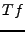 sera donc maximal en
sera donc maximal en 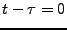 , donc en
, donc en 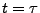 . Ceci permet
la mesure du temps inconnu
. Ceci permet
la mesure du temps inconnu 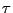 :
:
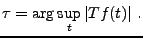 |
(3.51) |
Quant à la mesure de la constante 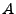 , elle s'effectue, une fois
, elle s'effectue, une fois 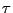 déterminé, via
déterminé, via
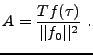 |
(3.52) |
Un exemple de détection utilisant le filtre adapté est montré en
FIG. ![[*]](crossref.png) .
.
REMARQUE 3.11 Notons que dans ce cas, la recherche de
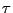
peut aussi se comprendre
de la façon suivante:
c'est à dire par une série de ``comparaisons'' (via le produit scalaire
de

) du signal

avec des copies translatées

du
signal de référence.
Figure:
Exemple de filtrage adapté:
Le signal de référence 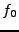 (à gauche)
a été décalé, et plongé dans un bruit blanc
(signal bruité au centre);
la sortie du filtre adapté (à droite) montre un maximum
clairement marqué,
qui donne une estimation du décalage.
(à gauche)
a été décalé, et plongé dans un bruit blanc
(signal bruité au centre);
la sortie du filtre adapté (à droite) montre un maximum
clairement marqué,
qui donne une estimation du décalage.
|
|
Considérons maintenant le cas  . On cherche toujours
à construire un système qui fournisse une réponse maximale
en
. On cherche toujours
à construire un système qui fournisse une réponse maximale
en 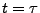 , mais il faut maintenant tenir compte de la perturbation
apportée par le bruit.
En effet, rien ne sert de construire un système
qui ``amplifierait'' le signal en
, mais il faut maintenant tenir compte de la perturbation
apportée par le bruit.
En effet, rien ne sert de construire un système
qui ``amplifierait'' le signal en 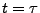 si celui-ci amplifie
également le bruit. Ceci conduit à normaliser la réponse du
système au bruit, de la façon suivante:
étant donné un filtre quelconque
si celui-ci amplifie
également le bruit. Ceci conduit à normaliser la réponse du
système au bruit, de la façon suivante:
étant donné un filtre quelconque 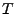 , on a alors
, on a alors
On dit que 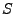 est le signal en sortie du filtre, et
est le signal en sortie du filtre, et 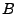 est le bruit
en sortie du filtre. On impose alors
est le bruit
en sortie du filtre. On impose alors 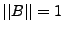 , c'est à dire, compte
tenu de la formule de Plancherel
, c'est à dire, compte
tenu de la formule de Plancherel
On est alors confronté à un problème de type (![[*]](crossref.png) ),
dans le cas
),
dans le cas
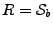 .
La solution est connue, et le filtre adapté est donné
par la formule suivante: pour tout
.
La solution est connue, et le filtre adapté est donné
par la formule suivante: pour tout
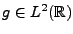 ,
,
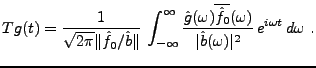 |
(3.53) |
De là, on obtient
et la valeur maximale de  est
est
Ce résultat permet donc a priori de déterminer  . Une fois que
. Une fois que
 a été déterminé, on peut alors en déduire la constante
a été déterminé, on peut alors en déduire la constante 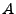 .
.
REMARQUE 3.12 Pour que cette approche ait un sens, c'est à dire pour retomber
dans le cadre décrit dans la section précédente,
il faut bien entendu faire des hypothèses sur
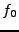
et
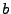
. Il faut
en particulier supposer
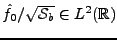
et
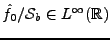
.
Le problème de la détection radar est encore plus complexe. En effet,
dans le cas du radar, le signal à détecter (généralement un signal
émis, qui a été réfléchi par une ``cible'' en mouvement)
est non seulement décalé dans le temps (d'une quantité proportionnelle
à la distance de la cible), mais aussi modulé, c'est à dire décalé
en fréquence par effet Doppler, d'une quantité proportionnelle à la vitesse
relative de la cible (tout au moins lorsque celle-ci est faible):
On peut également développer une théorie du filtrage optimal adaptée à
cette situation. Sans entrer dans les détails, considérons
la fonction (appelée fonction d'ambigüité) de deux variables
suivante
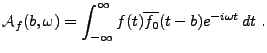 |
(3.54) |
Il est clair que d'après l'inégalité de Cauchy-Schwarz,
on a
Par conséquent, calculer numériquement la fonction d'ambigüité radar
d'un signal observé  et en rechercher les maxima fournit un
moyen d'estimer les paramètres inconnus
et en rechercher les maxima fournit un
moyen d'estimer les paramètres inconnus 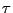 et
et 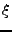 .
.
Les signaux numériques sont par définition des suites de
nombres, de longueur finie ou infinie. L'échantillonnage est
le problème d'associer à un signal analogique un signal numérique, en
contrôlant la perte d'information. La solution la plus simple revient
à considérer des valeurs ponctuelles 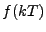 , régulièrement
espacées, du signal
, régulièrement
espacées, du signal  étudié. Cependant, ceci ne peut se faire sans
précautions; il faut tout d'abord que les valeurs ponctuelles aient un sens,
donc que
étudié. Cependant, ceci ne peut se faire sans
précautions; il faut tout d'abord que les valeurs ponctuelles aient un sens,
donc que  soit continue.
Puis pour limiter la perte d'information, il faut que
soit continue.
Puis pour limiter la perte d'information, il faut que  varie ``suffisamment lentement''. Ceci conduit à poser le
problème dans un cadre fonctionnel bien adapté.
On se limitera ici au cadre de la théorie de l'échantillonnage
classique, dans le cas des fonctions à bande limitée.
varie ``suffisamment lentement''. Ceci conduit à poser le
problème dans un cadre fonctionnel bien adapté.
On se limitera ici au cadre de la théorie de l'échantillonnage
classique, dans le cas des fonctions à bande limitée.
Le théorème d'échantillonnage se perd dans la nuit des temps.
Il est généralement attribué à Shannon et Kotelnikov,
qui en ont proposé une preuve vers 1945, peu après Nyquist.
En fait, il avait été démontré bien
avant par Whittaker (1936), et probablement par Cauchy encore plus avant.
Le cadre naturel du théorème d'échantillonnage est l'espace
des signaux à bande limitée, ou espace de Paley-Wiener
![$\displaystyle PW_{\omega_0} =\left\{f\in L^2({\mathbb{R}}), \hat f(\omega)=0\ \hbox{pour tout}\ \omega\not\in [-\omega_0,\omega_o]\right\}$](img1127.png) |
(3.55) |
Il est facile de voir que
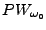 est un espace de fonctions continues,
de sorte que les valeurs ponctuelles des fonctions de
est un espace de fonctions continues,
de sorte que les valeurs ponctuelles des fonctions de
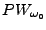 ont un sens.
On peut alors introduire l'opérateur d'échantillonnage
ont un sens.
On peut alors introduire l'opérateur d'échantillonnage 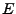 , associé
à la fréquence d'échantillonnage
, associé
à la fréquence d'échantillonnage 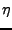 : si
: si
 ,
,
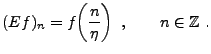 |
(3.56) |

Preuve:
Commençons par considérer la fonction périodique
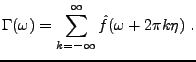 |
(3.57) |
Il est immédiat que
![$ \Gamma\in L^1_p([-\pi\eta,\pi\eta])$](img1134.png) , et on peut donc
s'intéresser à ses coefficients de Fourier. Un calcul simple montre que
, et on peut donc
s'intéresser à ses coefficients de Fourier. Un calcul simple montre que
Donc, la fonction 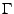 n'est autre que la TFD
de la série d'échantillons
n'est autre que la TFD
de la série d'échantillons
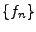 , et le problème de retrouver
, et le problème de retrouver  à partir des échantillons
est équivalent au problème de retrouver
à partir des échantillons
est équivalent au problème de retrouver 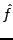 à partir de
à partir de 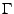 .
Or,
.
Or, 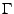 n'est autre (à une constante multiplicative près) qu'une
version ``périodisée'' de
n'est autre (à une constante multiplicative près) qu'une
version ``périodisée'' de 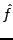 , de période
, de période 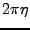 . On peut
donc considérer les trois cas de figure.
. On peut
donc considérer les trois cas de figure.
- Supposons que
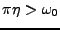 . Alors, il est clair que
l'on peut toujours trouver une fonction
. Alors, il est clair que
l'on peut toujours trouver une fonction 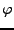 , dont la transformée
de Fourier
, dont la transformée
de Fourier
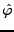 est
est  , à support compact dans
l'intervalle
, à support compact dans
l'intervalle
![$ [-\omega_0,\omega_0]$](img1140.png) , et vaut uniformément 1 dans
, et vaut uniformément 1 dans
![$ [-\pi\eta,\pi\eta]$](img1141.png) . On a donc
. On a donc
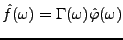 , ce qui se
traduit, après transformation de Fourier inverse, par
la relation (
, ce qui se
traduit, après transformation de Fourier inverse, par
la relation (![[*]](crossref.png) ).
).
- Dans le cas critique, le raisonnement est similaire, à ceci près
que la fonction
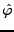 ne peut plus être choisie continue, et est
nécessairement de la forme
ne peut plus être choisie continue, et est
nécessairement de la forme
![$ \varphi(\omega)=\chi_{[-\omega_0,\omega_0]}(\omega)$](img1143.png) . La
transformée de Fourier inverse de cette dernière étant
le sinus cardinal, on obtient (
. La
transformée de Fourier inverse de cette dernière étant
le sinus cardinal, on obtient (![[*]](crossref.png) ).
).
- Si
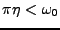 , le ``truc'' précédent ne
fonctionne plus: la périodisation ``mélange des morceaux de
, le ``truc'' précédent ne
fonctionne plus: la périodisation ``mélange des morceaux de 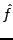 congrus modulo
congrus modulo 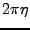 , de sorte que l'on ne peut plus inverser le
processus. C'est le phénomène de repliement de spectre.
, de sorte que l'on ne peut plus inverser le
processus. C'est le phénomène de repliement de spectre.
Ceci conclut la démonstration.

Le cas critique
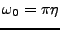 est particulièrement
intéressant, et il est utile de reprendre les résultats
précédents, sous un angle différent.
L'opérateur
est particulièrement
intéressant, et il est utile de reprendre les résultats
précédents, sous un angle différent.
L'opérateur
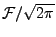 est une isométrie bijective
entre
est une isométrie bijective
entre
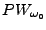 et
et
![$ L^2([-\omega_0,\omega_0])$](img1147.png) .
Or, nous connaissons une base orthonormée de ce dernier espace:
le système trigonométrique. Par conséquent, la famille de
fonctions
.
Or, nous connaissons une base orthonormée de ce dernier espace:
le système trigonométrique. Par conséquent, la famille de
fonctions 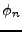 définies par
définies par
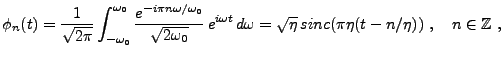 |
(3.58) |
où on a introduit le sinus cardinal
 |
(3.59) |
est une base orthonormée de
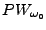 .
On a donc le résultat suivant
.
On a donc le résultat suivant
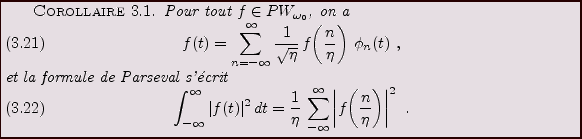
De plus, la transformation de Fourier sur
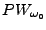 se ramène à
une transformation de Fourier discrète (TFD) de la suite des échantillons:
se ramène à
une transformation de Fourier discrète (TFD) de la suite des échantillons:
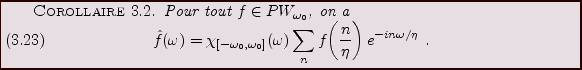
REMARQUE 3.13 Dans le cas favorable
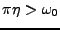
, la famille de fonctions

considérée n'est plus une
base orthonormée, car elle est redondante. On peut alors montrer
qu'elle forme alors un repère de
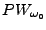
.
REMARQUE 3.14 En pratique, l'échantillonnage est souvent (toujours) précédé
d'un filtrage passe-bas, dont le but est de réduire la largeur
de bande pour l'adapter à la fréquence d'échantillonnage prévue.
Les filtres passe-bas idéaux n'étant pas réalisables, on se
rabat plutôt sur des filtres rationnels, comme par exemple
un des filtres de Chebyshev ou de Butterworth que nous avons vus plus haut.
Nous avons vu que les espaces de Paley-Wiener sont particulièrement
bien adaptés à l'échantillonnage. Soit
 , et soit
, et soit
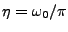 .
Reprenant ce que nous avons vu plus haut, nous pouvons donc écrire,
pour tout
.
Reprenant ce que nous avons vu plus haut, nous pouvons donc écrire,
pour tout 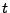 ,
,
et nous intéresser aux séries tronquées
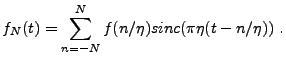 |
(3.60) |
Nous avons alors le résultat suivant

Preuve:
La première relation est une conséquence immédiate de la formule de
Parseval vue dans le Corollaire ![[*]](crossref.png) . Pour la seconde,
écrivons
. Pour la seconde,
écrivons
ce qui conclut la preuve.

La contrepartie du corollaire ![[*]](crossref.png) est que la
transformée de Fourier peut maintenant s'approximer par une TFF,
très facile à réaliser numériquement.
est que la
transformée de Fourier peut maintenant s'approximer par une TFF,
très facile à réaliser numériquement.
Comme on l'a vu, le théorème d'échantillonnage, dans le cas critique
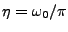 , peut être interprété comme la représentation
d'une fonction (continue, appartenant à l'espace de Paley-Wiener)
par les coefficients de son développement sur la base des sinus cardinaux.
, peut être interprété comme la représentation
d'une fonction (continue, appartenant à l'espace de Paley-Wiener)
par les coefficients de son développement sur la base des sinus cardinaux.
Ceci peut être généralisé, dès lors que l'on se donne un
sous-espace fermé de
 et une base de ce sous-espace.
Un choix classique consiste à considérer une fonction
et une base de ce sous-espace.
Un choix classique consiste à considérer une fonction
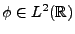 ,
et le sous-espace engendré par les translatées régulières
,
et le sous-espace engendré par les translatées régulières
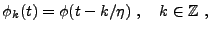 |
(3.61) |
(
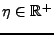 étant une fréquence d'échantillonnage fixée),
c'est à dire l'espace
étant une fréquence d'échantillonnage fixée),
c'est à dire l'espace
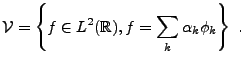 |
(3.62) |
Si la fonction 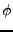 et la fréquence d'échantillonnage sont
bien choisies, la collection des
et la fréquence d'échantillonnage sont
bien choisies, la collection des 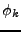 forme une base de Riesz de
forme une base de Riesz de
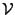 ,
et toute fonction
,
et toute fonction
 peut être caractérisée par les coefficients
peut être caractérisée par les coefficients
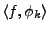 . Plus précisément, on peut montrer le
résultat suivant:
. Plus précisément, on peut montrer le
résultat suivant:
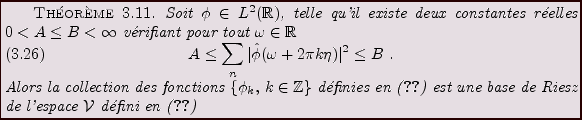
REMARQUE 3.15 Notons que le calcul des coefficients d'une fonction

par rapport
à une telle base prend la forme
ce qui peut s'interpréter comme
où
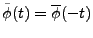
, c'est à dire comme
filtrage par un filtre de réponse impulsionnelle
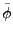
, suivi
d'un échantillonnage à fréquence
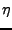
.
REMARQUE 3.16 Il est possible de traiter de façon similaire des situations où la suite
des translatées
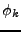
n'est pas une base, mais un repère de l'espace
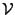
.
Bruno Torresani
2007-06-26
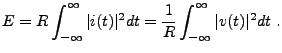
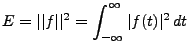
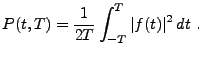
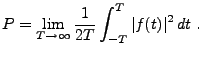
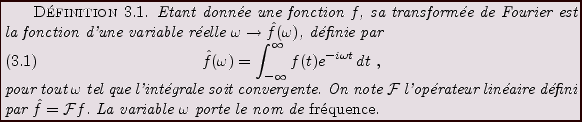
![\begin{theorem}[Riemann-Lebesgue]
Soit $f\in L^1({\mathbb{R}})$. Alors $\hat f$\...
...h}
\lim_{\omega\to\pm\infty}\hat f(\omega) = 0\ .
\end{displaymath}\end{theorem}](img715.png)
![]() , alors
, alors ![]() est bornée.
Passons à la continuité.
La preuve est relativement simple. Commençons par calculer
est bornée.
Passons à la continuité.
La preuve est relativement simple. Commençons par calculer

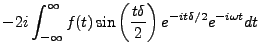
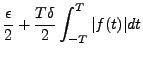
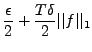
![[*]](crossref.png) ).
La première partie du théorème est donc montrée.
).
La première partie du théorème est donc montrée.
![]() quand
quand
![]() résulte de la densité des fonctions constantes par morceaux
dans l'espace
résulte de la densité des fonctions constantes par morceaux
dans l'espace
![]() : pour toute fonction
: pour toute fonction
![]() , il existe
une suite de fonctions
, il existe
une suite de fonctions ![]() , constantes par morceaux, telle que
pour tout
, constantes par morceaux, telle que
pour tout ![]() fixé, on ait
fixé, on ait
![]() pour
un
pour
un ![]() assez grand. Il suffit donc d'étudier le comportement
de la fonction caractéristique d'un intervalle; prenons
assez grand. Il suffit donc d'étudier le comportement
de la fonction caractéristique d'un intervalle; prenons
![]() . Alors, on a
. Alors, on a
![]() , qui tend bien vers 0 quand
, qui tend bien vers 0 quand
![]() .
De même, la transformée de Fourier de toute fonction intégrable
constante par morceaux tend vers 0 à l'infini. Pour conclure, il
suffit de remarquer que pour tout
.
De même, la transformée de Fourier de toute fonction intégrable
constante par morceaux tend vers 0 à l'infini. Pour conclure, il
suffit de remarquer que pour tout ![]() , on a par hypothèse
, on a par hypothèse
![]() . Comme pour tout
. Comme pour tout ![]() ,
,
![]() quand
quand
![]() , et comme
, et comme
![]() peut
être rendu aussi prôche de 0 que ce que l'on veut, on en déduit
que
peut
être rendu aussi prôche de 0 que ce que l'on veut, on en déduit
que
![]() quand
quand
![]() .
.
![]()
![]() pour simplifier (ce qui
assure l'existence de
pour simplifier (ce qui
assure l'existence de
![]() pour tout
pour tout ![]() , on
vérifie facilement les propriétés suivantes:
, on
vérifie facilement les propriétés suivantes:
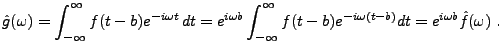
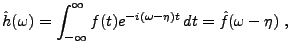
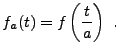
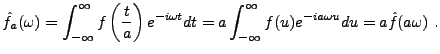
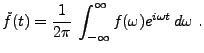
![\begin{lemma}[Formule d'\'echange]
Soient $f,g\in L^1({\mathbb{R}})$. Alors on a...
...ion}
\int f(t)\hat g(t) dt = \int \hat f(s) g(s) ds\ .
\end{equation}\end{lemma}](img756.png)
![]()
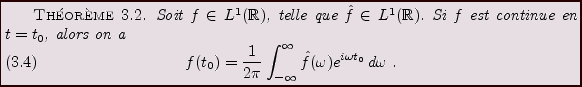
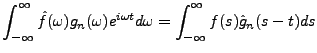
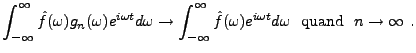
![[*]](crossref.png) ), nous sommes amenés à considérer
), nous sommes amenés à considérer
![$\displaystyle \left\vert\int_{\vert s\vert\le\rho}\left[f(s+t_0)-f(t_0)\right]\...
...ert
\le \epsilon \int_{\vert s\vert\le\rho} \hat g_n(s) ds\le 2\pi \epsilon\ ,
$](img771.png)
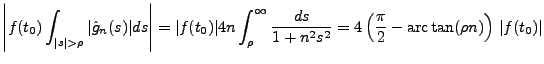

![[*]](crossref.png) ), au point de continuité
), au point de continuité 
![]() et multiplication par
et multiplication par ![]() de
de ![]() . Supposons que
. Supposons que
![]() , et que de plus la fonction
, et que de plus la fonction
![]() appartienne elle aussi
à
appartienne elle aussi
à
![]() . Comme dans la preuve du théorème de Riemann-Lebesgue, on a
. Comme dans la preuve du théorème de Riemann-Lebesgue, on a

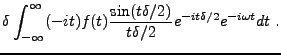
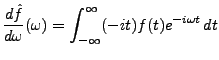

 = (i\omega)^k \hat f(\omega)\ .
\end{equation}\end{proposition}](img783.png)
![]() satisfaisant aux hypothèses du théorème, et remarquons tout
d'abord que comme
satisfaisant aux hypothèses du théorème, et remarquons tout
d'abord que comme ![]() est supposée intégrable, on a
est supposée intégrable, on a
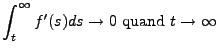
![$\displaystyle \int_{-\infty}^\infty f'(t)e^{-i\omega t} dt = \left[-i\omega f(t)\right]_{-\infty}^\infty
+ i\omega \int_{-\infty}^\infty f(t)e^{-i\omega t} dt
$](img788.png)
![[*]](crossref.png) fournit un exemple d'un comportement
général de la transformation de Fourier: plus une fonction est
régulière, plus sa transformée de Fourier est rapidement décroissante.
Dans le cas particulier, si toutes les dérivées de
fournit un exemple d'un comportement
général de la transformation de Fourier: plus une fonction est
régulière, plus sa transformée de Fourier est rapidement décroissante.
Dans le cas particulier, si toutes les dérivées de 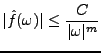
![]() , d'employer des moyens détournés, à savoir des arguments
de densité.
Commençons par considérer l'espace des fonctions
, d'employer des moyens détournés, à savoir des arguments
de densité.
Commençons par considérer l'espace des fonctions ![]() à support borné
à support borné
![\begin{definition}[Fonction \\lq a d\'ecroissance rapide]
Soit $f$\ une fonction co...
...n}
\vert f(t)\vert \le \frac{C_k}{\vert t\vert^k}
\end{equation}\end{definition}](img802.png)
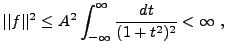

![]() est lui aussi dense
dans
est lui aussi dense
dans
![]() . C'est sur cette propriété que nous allons nous
appuyer pour étendre la transformation de Fourier à
. C'est sur cette propriété que nous allons nous
appuyer pour étendre la transformation de Fourier à
![]() .
.
![]() possède une propriété remarquable:
la transformée de Fourier d'une fonction appartenant à
possède une propriété remarquable:
la transformée de Fourier d'une fonction appartenant à
![]() est
elle aussi une fonction de
est
elle aussi une fonction de
![]() . Pour nous en convaincre,
commençons par faire les remarques suivantes:
. Pour nous en convaincre,
commençons par faire les remarques suivantes:
![]() , et la discussion
précédente s'applique tout aussi bien à
, et la discussion
précédente s'applique tout aussi bien à ![]() . Par conséquent,
nous avons montré
. Par conséquent,
nous avons montré
![]()
![]() , et posons
, et posons
![]() .
Alors un calcul simple montre que
.
Alors un calcul simple montre que
![]() .
Appliquons la formule d'échange à
.
Appliquons la formule d'échange à ![]() et
et ![]() . Ceci nous donne la
formule de Plancherel:
. Ceci nous donne la
formule de Plancherel:
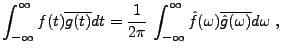
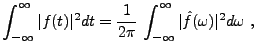

![\begin{theorem}[Transformation de Fourier sur $L^2({\mathbb{R}})$]
La transforma...
...y \hat f(\omega) \overline{\hat g(\omega)}d\omega\ .
\end{equation}\end{theorem}](img837.png)
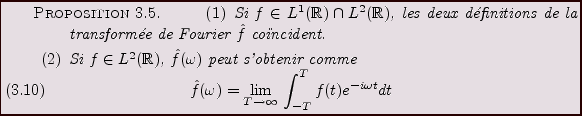
![[*]](crossref.png) )
)
![]() , on peut
écrire
, on peut
écrire
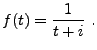
![\begin{theorem}[Heisenberg-Wiener]
Soit $f\in L^2({\mathbb{R}})$, $f\ne 0$. On p...
...{displaymath}
f(t) = a e^{ib t} e^{-(t-c)^2/d}\ .
\end{displaymath}\end{theorem}](img850.png)
![$\displaystyle \int_u^v t \frac{d}{dt} \vert f(t)\vert^2 dt= \left[ t\vert f(t)\vert^2\right]_u^v
- \int_u^v \vert f(t)\vert^2 dt\ .
$](img854.png)
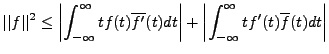
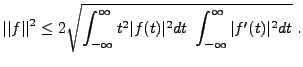
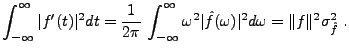
![]() définie par
définie par
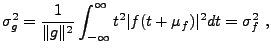
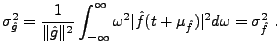
![\begin{proposition}[Paley-Wiener]
Soit $f\in L^2({\mathbb{R}})$\ une fonction no...
...pport compact, alors $f$\ ne
peut s'annuler sur un intervalle.
\end{proposition}](img870.png)
![]() soit inclus dans
soit inclus dans ![]() , et que pour
tout
, et que pour
tout
![]() , on ait
, on ait ![]() . Soit
. Soit ![]() . On sait que
. On sait que
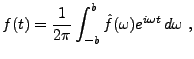
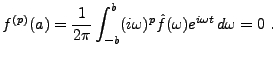
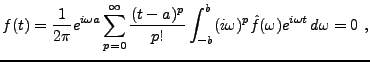
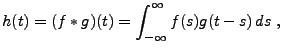
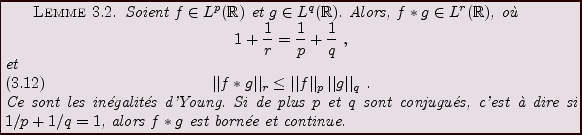
![[*]](crossref.png) ) est
donc valable point par point.
) est
donc valable point par point.
![[*]](crossref.png) ), et considérons le cas simple
), et considérons le cas simple
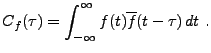
![]() , considérons la fonction définie par
, considérons la fonction définie par
![]() ,
,
![]() , et
, et
![]() est intégrable.
Donc, sa transformée de Fourier inverse a un sens, et définit une
fonction bornée continue. Ainsi, on a
est intégrable.
Donc, sa transformée de Fourier inverse a un sens, et définit une
fonction bornée continue. Ainsi, on a
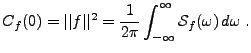
![[*]](crossref.png) ).
).
![]() une fonction, telle que
une fonction, telle que
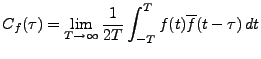
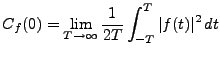
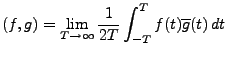
![[*]](crossref.png) .
.
![$\displaystyle \frac1{2T}\int_{-T}^T f(t)\overline{g}(t)\,dt\le
\left[\frac1{2T}...
...ight]^{1/2}
\left[\frac1{2T}\int_{-T}^T \vert g(t)\vert^2\, dt\right]^{1/2}\ ,
$](img928.png)

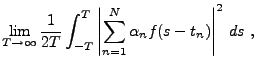
![\begin{theorem}[Bochner]
Soit $F$\ une fonction d\'efinie non-n\'egative,
contin...
...\int_{-\infty}^\infty e^{i\omega t} d\nu (\omega)\ .
\end{equation}\end{theorem}](img939.png)
![]() :
:
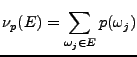
![[*]](crossref.png) ).
).
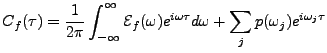
![]() , comment l'approximer par un filtre
réalisable par un circuit électronique.
, comment l'approximer par un filtre
réalisable par un circuit électronique.
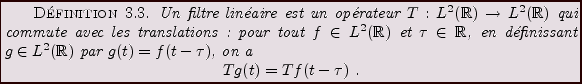
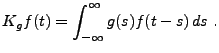
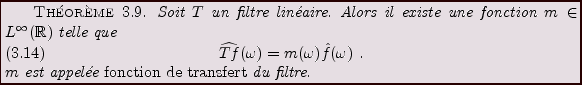

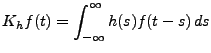
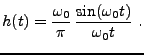
![[*]](crossref.png) .
.
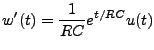
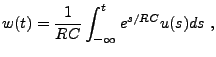
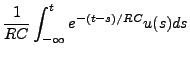
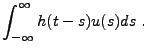
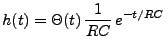
![]() et la sortie
et la sortie ![]() sont liés par une équation différentielle du type
sont liés par une équation différentielle du type
![]()
![]() les racines (complexes) de
les racines (complexes) de ![]() , et
soit
, et
soit ![]() leur multiplicité:
leur multiplicité:

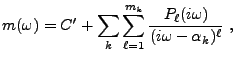
![]() , où
, où
![]() .
Un calcul immédiat donne
.
Un calcul immédiat donne
![]() .
Plus généralement, si
.
Plus généralement, si
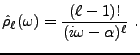

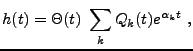
![]() de
de ![]() , on ait
, on ait
![]() . Un calcul similaire au précédent
montre que la transformée de Fourier inverse de
. Un calcul similaire au précédent
montre que la transformée de Fourier inverse de
![]() est proportionnelle
à
est proportionnelle
à
![]() , ce qui est incompatible avec la causalité.
Ceci achève la preuve de la proposition.
, ce qui est incompatible avec la causalité.
Ceci achève la preuve de la proposition.
![]()
![]()
![]() une racine de
une racine de ![]() . D'après la
parité de
. D'après la
parité de ![]() ,
, ![]() est également racine de
est également racine de ![]() . Si
. Si ![]() est
complexe,
est
complexe,
![]() et
et
![]() sont également
racines. Si
sont également
racines. Si
![]() et
et
![]() ,
,
![]() contient nécessairement un terme de la forme
contient nécessairement un terme de la forme
![]() , alors
, alors ![]() est nécessairement
de multiplicité paire: en effet,
est nécessairement
de multiplicité paire: en effet, ![]() contient obligatoirement
un terme en
contient obligatoirement
un terme en
![]() ,
, ![]() étant la multiplicité
de
étant la multiplicité
de ![]() , et pour que
, et pour que ![]() soit positif
soit positif ![]() doit nécessairement
être pair. Donc
doit nécessairement
être pair. Donc
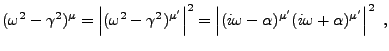
![]() ,
, ![]() contient nécessairement
un terme en
contient nécessairement
un terme en
![]() , qui est toujours positif,
et de la forme
, qui est toujours positif,
et de la forme
![]() une fonction rationnelle de
une fonction rationnelle de ![]() , de la forme
, de la forme

![[*]](crossref.png) montre qu'il est possible de se limiter dans ce cas à des racines
de partie réelle négative (le fait que la fraction rationnelle
considérée soit bornée implique que le dénominateur n'a aucune
racine imaginaire pure).
montre qu'il est possible de se limiter dans ce cas à des racines
de partie réelle négative (le fait que la fraction rationnelle
considérée soit bornée implique que le dénominateur n'a aucune
racine imaginaire pure).
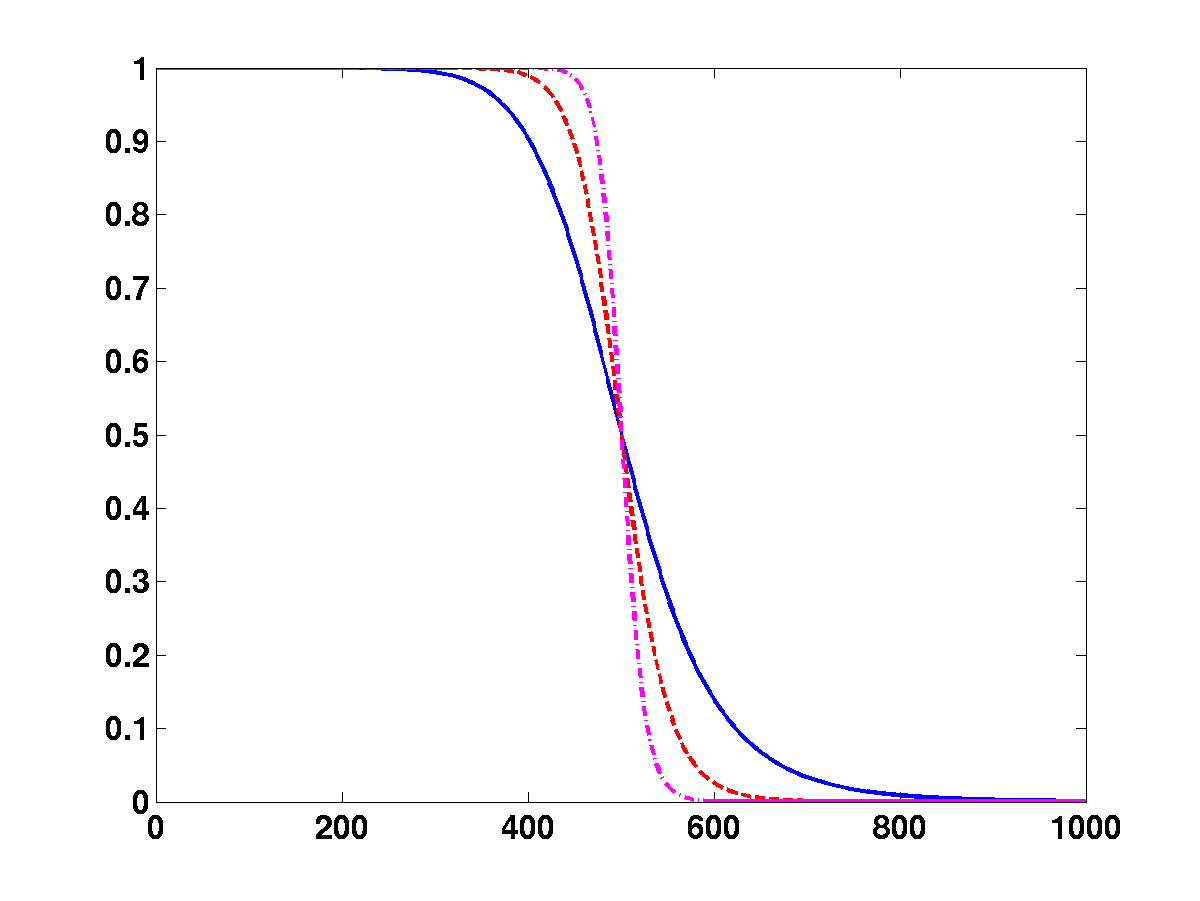
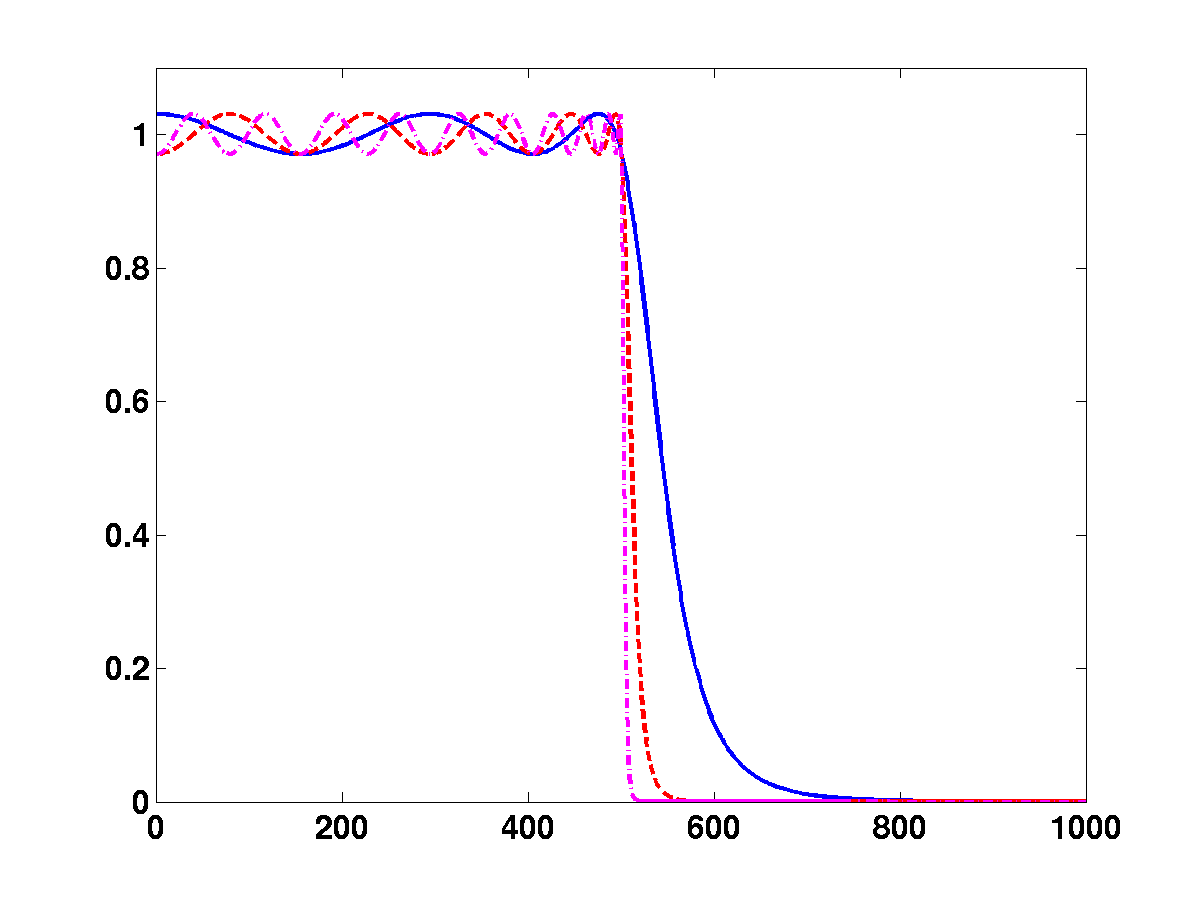
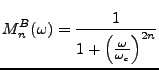
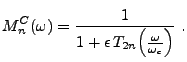
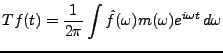
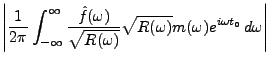
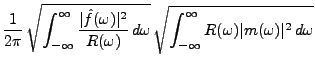
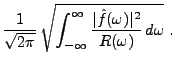
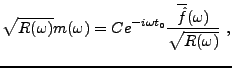
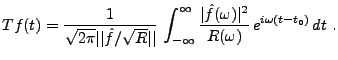
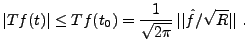

![]() . On commence alors
par construire un système linéaire
. On commence alors
par construire un système linéaire ![]() tel que
tel que
![]() soit le plus grand possible. La solution nous est donnée
par la théorie ci-dessus:
soit le plus grand possible. La solution nous est donnée
par la théorie ci-dessus: ![]() , où
, où ![]() est définie par
est définie par
![]() . On sait de plus que pour tout
. On sait de plus que pour tout ![]() ,
,
![]() .
Alors, compte tenu du fait que le filtre
.
Alors, compte tenu du fait que le filtre ![]() est linéaire et
commute avec les translations, on sait que
est linéaire et
commute avec les translations, on sait que
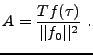
![[*]](crossref.png) .
.
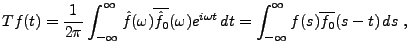
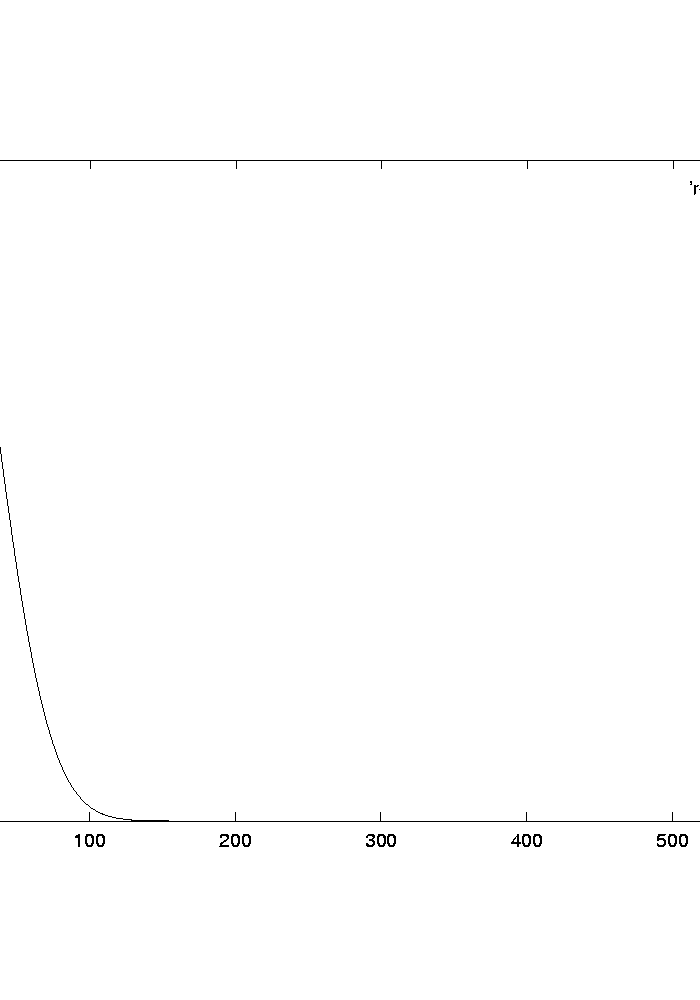
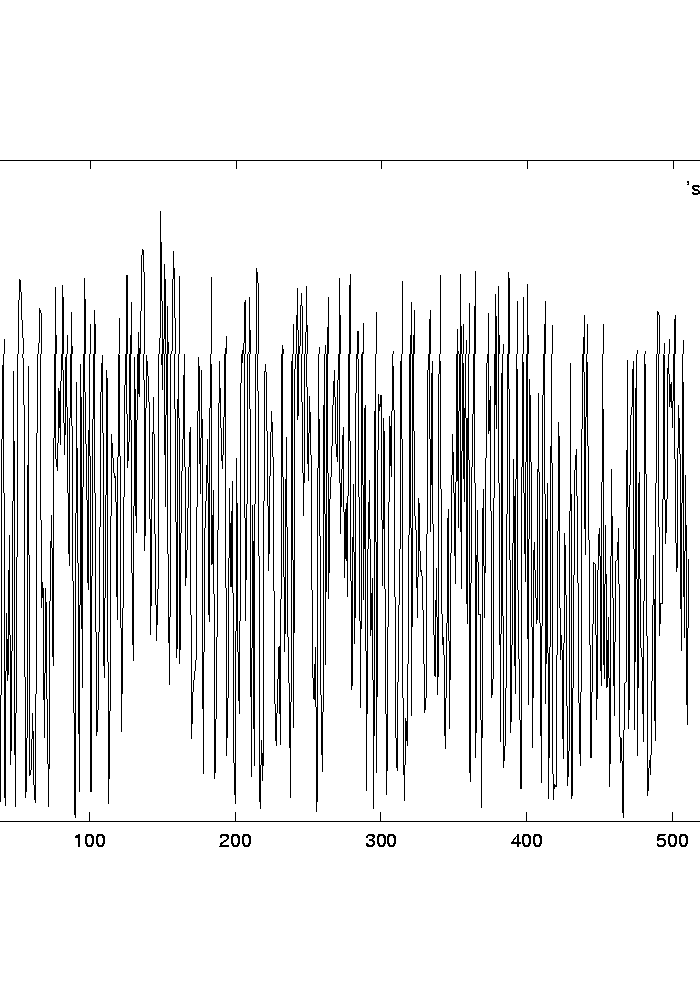
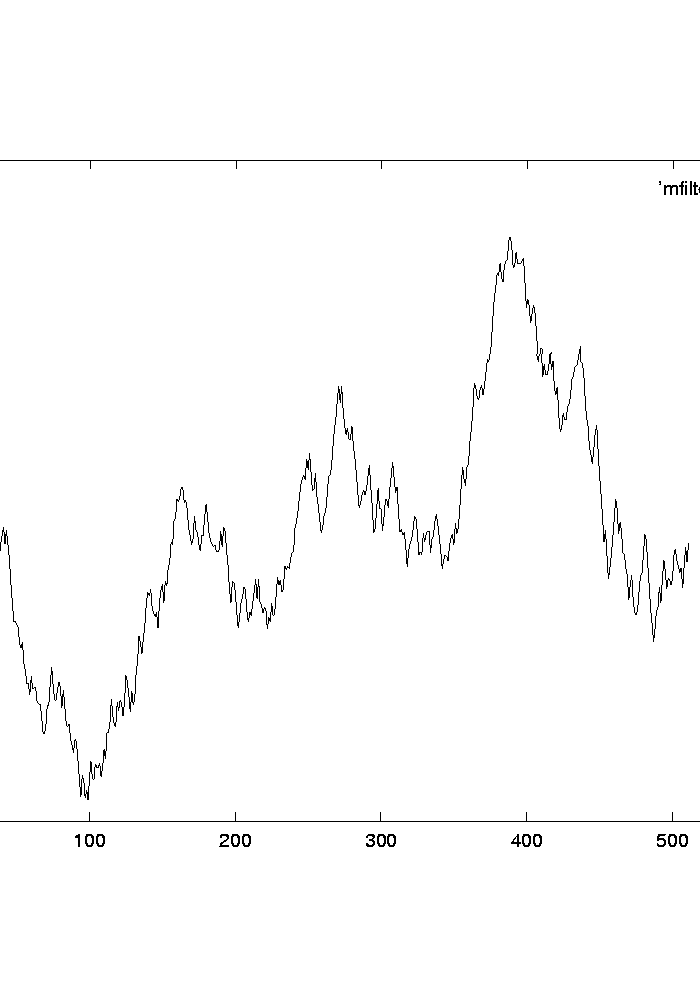
![]() . On cherche toujours
à construire un système qui fournisse une réponse maximale
en
. On cherche toujours
à construire un système qui fournisse une réponse maximale
en ![]() , mais il faut maintenant tenir compte de la perturbation
apportée par le bruit.
En effet, rien ne sert de construire un système
qui ``amplifierait'' le signal en
, mais il faut maintenant tenir compte de la perturbation
apportée par le bruit.
En effet, rien ne sert de construire un système
qui ``amplifierait'' le signal en ![]() si celui-ci amplifie
également le bruit. Ceci conduit à normaliser la réponse du
système au bruit, de la façon suivante:
étant donné un filtre quelconque
si celui-ci amplifie
également le bruit. Ceci conduit à normaliser la réponse du
système au bruit, de la façon suivante:
étant donné un filtre quelconque ![]() , on a alors
, on a alors
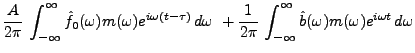
![[*]](crossref.png) ),
dans le cas
),
dans le cas
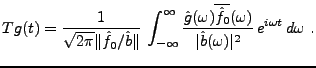
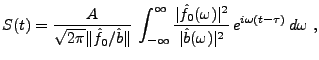
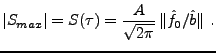
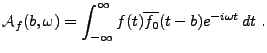

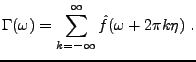
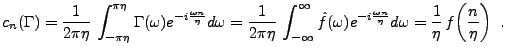
![[*]](crossref.png) ).
).
![[*]](crossref.png) ).
).
![]() est particulièrement
intéressant, et il est utile de reprendre les résultats
précédents, sous un angle différent.
L'opérateur
est particulièrement
intéressant, et il est utile de reprendre les résultats
précédents, sous un angle différent.
L'opérateur
![]() est une isométrie bijective
entre
est une isométrie bijective
entre
![]() et
et
![]() .
Or, nous connaissons une base orthonormée de ce dernier espace:
le système trigonométrique. Par conséquent, la famille de
fonctions
.
Or, nous connaissons une base orthonormée de ce dernier espace:
le système trigonométrique. Par conséquent, la famille de
fonctions ![]() définies par
définies par
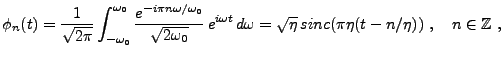

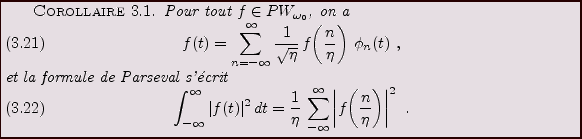
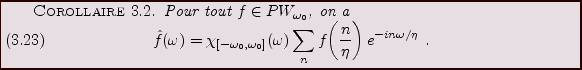
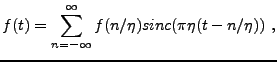
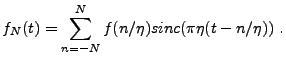

![[*]](crossref.png) . Pour la seconde,
écrivons
. Pour la seconde,
écrivons
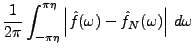
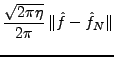
![[*]](crossref.png) est que la
transformée de Fourier peut maintenant s'approximer par une TFF,
très facile à réaliser numériquement.
est que la
transformée de Fourier peut maintenant s'approximer par une TFF,
très facile à réaliser numériquement.
![]() et une base de ce sous-espace.
Un choix classique consiste à considérer une fonction
et une base de ce sous-espace.
Un choix classique consiste à considérer une fonction
![]() ,
et le sous-espace engendré par les translatées régulières
,
et le sous-espace engendré par les translatées régulières