Sous-sections
Le traitement du signal classique s'appuie fortement sur
l'analyse harmonique, et en particulier l'analyse de Fourier.
On donne ici les éléments essentiels de la théorie des
séries de Fourier, avant d'appliquer les résultats
essentiels au traitement des signaux numériques.
Séries de Fourier
Commençons par introduire les espaces
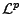 : soient
: soient 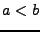 deux réels,
et soit
deux réels,
et soit  une fonction:
une fonction:
![$ f: [a,b]\to\mathbb{C}$](img7.png) . On dit que
. On dit que
![$ f\in{\mathcal L}^p([a,b])$](img8.png) si
si
L'application
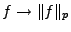 définit une seminorme sur
définit une seminorme sur
![$ {\mathcal L}^p([a,b])$](img11.png) ,
seminorme qui peut être transformée en norme par un passage au
quotient approprié. Etant données
,
seminorme qui peut être transformée en norme par un passage au
quotient approprié. Etant données
![$ f,g\in {\mathcal L}^p([a,b])$](img12.png) , on dira que
, on dira que
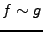 si
si
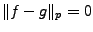 . Ceci définit une relation d'équivalence,
et on peut alors définir
. Ceci définit une relation d'équivalence,
et on peut alors définir
![$ L^p([a,b])$](img15.png) par
par
c'est à dire en identifiant les fonctions qui diffèrent sur un ensemble
de mesure nulle. On montre que la norme ainsi obtenue munit
![$ L^p([a,b])$](img15.png) d'une structure d'espace de Banach.
d'une structure d'espace de Banach.
Soit
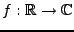 . On dira que
. On dira que
![$ f\in L^q_p([a,b])$](img18.png) si la restriction de
si la restriction de
 à l'intervalle
à l'intervalle ![$ [a,b]$](img19.png) appartient à
appartient à
![$ L^q([a,b])$](img20.png) , et si
, et si  est
périodique dans le sens suivant: en posant
est
périodique dans le sens suivant: en posant  , et
, et
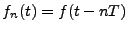 ,
on a
,
on a 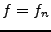 pour tout
pour tout 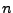 .
.
On définit de façon analogue les espaces
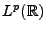 .
.
On dit qu'une suite
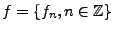 appartient à
appartient à
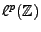 si
si
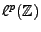 est lui aussi naturellement muni d'une structure d'espace de
Banach par la norme
est lui aussi naturellement muni d'une structure d'espace de
Banach par la norme 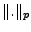 .
.
Les espaces
![$ L^p([a,b])$](img15.png) et
et
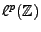 possèdent des propriétés
simples d'inclusion:
possèdent des propriétés
simples d'inclusion:
Preuve :
1) Soit
![$ f\in L^p([a,b])$](img31.png) , et soit
, et soit 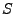 l'ensemble des points
l'ensemble des points  tels
que
tels
que
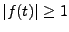 . Sur
. Sur 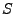 , on a alors
, on a alors
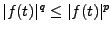 pour
tout
pour
tout 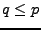 . On a alors, en notant
. On a alors, en notant ![$ I=[a,b]$](img37.png) ,
,
2) Le cas des suites est une conséquence directe du critère de
Riemann.

REMARQUE 1.1 Il est à noter que dans le cas des espaces
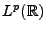
, il n'existe
aucune relation d'inclusion de telle sorte.
On définit de la façon usuelle le produit simple des suites
(
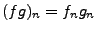 ) et des fonctions (
) et des fonctions (
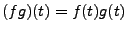 );
on utilisera régulièrement le résultat suivant
);
on utilisera régulièrement le résultat suivant
![\begin{proposition}[H\uml older]
\index{In \'egalit\'e de H\ölder}
Soient $1\le ...
...g\Vert _r\le \Vert f\Vert _p\,\Vert g\Vert _q\ .
\end{equation}\end{proposition}](img42.png)
Considérons l'espace
![$ L^2_p([a,b])$](img44.png) des fonctions périodiques de période
des fonctions périodiques de période 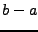 , de carré
intégrable sur l'intervalle
, de carré
intégrable sur l'intervalle ![$ [a,b]$](img19.png) (et donc sur tout intervalle
de longueur
(et donc sur tout intervalle
de longueur 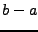 ), muni du produit scalaire
), muni du produit scalaire
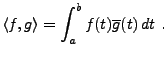 |
(1.1) |
On considère les fonctions trigonométriques
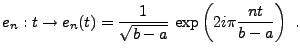 |
(1.2) |
On vérifie facilement que la famille de fonctions
 est
un système orthonormal dans
est
un système orthonormal dans
![$ L^2_p([a,b])$](img44.png) . Pour montrer qu'il s'agit
d'une base orthonormale, il nous suffit donc de montrer que
le système est complet.
. Pour montrer qu'il s'agit
d'une base orthonormale, il nous suffit donc de montrer que
le système est complet.
Une première méthode consiste à utiliser la densité de
![$ C([a,b])$](img49.png) dans
dans
![$ L^2([a,b])$](img50.png) . On peut alors utiliser
le résultat d'approximation des fonctions
continues par des polynômes trigonométriques (voir [7])
pour une démonstration):
. On peut alors utiliser
le résultat d'approximation des fonctions
continues par des polynômes trigonométriques (voir [7])
pour une démonstration):
![\begin{proposition}[Weierstrass]
Soit $f\in C([a,b])$. Pour tout $\epsilon >0$, ...
...in{equation}
\vert f(t) -P(t)\vert\le\epsilon\ .
\end{equation}\end{proposition}](img51.png)
Supposons pour simplifier que
![$ [a,b]=[-\pi,\pi]$](img52.png) (le cas général
se traite de façon similaire).
Soit
(le cas général
se traite de façon similaire).
Soit
![$ f\in L^1([-\pi,\pi])$](img53.png) , et supposons que
, et supposons que  soit orthogonale
à toutes les fonctions
soit orthogonale
à toutes les fonctions  :
:
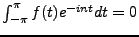 ,
,
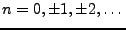 .
Soit
.
Soit 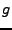 définie par
définie par
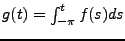 .
. 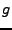 est continue par construction,
et vérifie
est continue par construction,
et vérifie 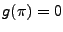 .
Si
.
Si 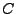 est une constante
complexe quelconque, une intégration par parties montre que
est une constante
complexe quelconque, une intégration par parties montre que
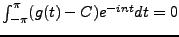 ,
,
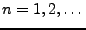 . Un choix adéquat de
. Un choix adéquat de
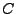 permet à cette égalité d'être valide pour
permet à cette égalité d'être valide pour 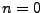 également.
On pose alors
également.
On pose alors
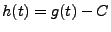 .
.
![$ h\in C([-\pi,\pi])$](img65.png) , et on sait
d'après le résultat ci-dessus que pour tout
, et on sait
d'après le résultat ci-dessus que pour tout
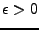 , il existe
un polynôme trigonométrique
, il existe
un polynôme trigonométrique 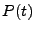 tel que pour tout
tel que pour tout
![$ t\in [-\pi,\pi]$](img68.png) ,
,
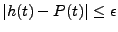 . Donc, on a
. Donc, on a
d'où on déduit que pour tout
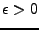 ,
,
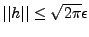 .
Donc
.
Donc 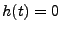 presque partout,
presque partout,
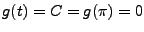 pour presque tout
pour presque tout
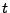 , et donc
, et donc 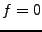 .
On a ainsi, comme pour tout
.
On a ainsi, comme pour tout 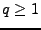 ,
,
![$ L^q([-\pi,\pi]) \subset L^1([-\pi,\pi])$](img76.png) , le résultat suivant
, le résultat suivant
![\begin{corollary}
Le syst\\lq eme trigonom\'etrique est complet dans $L^2_p([-\pi,\pi])$.
\end{corollary}](img77.png)
REMARQUE 1.2 En fait, on peut également utiliser directement la densité de
![$ C([a,b])$](img49.png)
dans
![$ L^2([a,b])$](img50.png)
.
Nous sommes donc en position d'utiliser les résultats précédents, ce
qui conduit aux séries de Fourier. Pour tout
![$ f\in L^2([a,b])$](img78.png) , on pose
, on pose
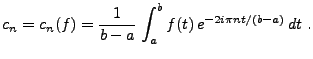 |
(1.3) |
Les nombres 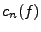 (qui existent puisque
(qui existent puisque
![$ L^2([a,b])\subset L^1([a,b])$](img81.png) sont appelés coefficients de Fourier
de
sont appelés coefficients de Fourier
de  , et on s'intéresse aux sommes partielles
, et on s'intéresse aux sommes partielles
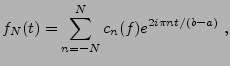 |
(1.4) |
ainsi qu'à leur limite
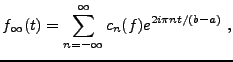 |
(1.5) |
appelée série de Fourier de  .
.
Il résulte de la discussion précédente (et en particulier du
théorème ![[*]](crossref.png) de l'Appendice
de l'Appendice ![[*]](crossref.png) )
que si
)
que si
![$ f\in L^2_p([a,b])$](img84.png) , la suite
, la suite
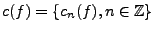 appartient à
appartient à
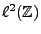 , et la série de Fourier
, et la série de Fourier
converge au sens de 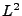 . On a donc
. On a donc

REMARQUE 1.3 Les séries de Fourier fournissent des décompositions des fonctions
périodiques ou à support borné comme superpositions de ``briques''
élémentaires, les fonctions
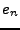
. La variable
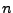
possède une
signification ``physique'' essentielle: il s'agit d'une variable
de fréquence, qui par exemple dans le cas où la fonction

étudiée
représente un son, caractérise la ``hauteur'' du son. Les grands
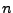
(hautes fréquences) correspondent aus sons aigus, et les faibles
valeurs de
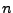
aux sons graves.
La théorie 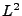 ne donne que des indications relativement limitées
sur le comportement des coefficients de Fourier, et sur
la convergence des séries de Fourier. Par exemple, la formule de
Parseval implique que si
ne donne que des indications relativement limitées
sur le comportement des coefficients de Fourier, et sur
la convergence des séries de Fourier. Par exemple, la formule de
Parseval implique que si
![$ f\in L^2_p([a,b])$](img84.png) , alors
, alors
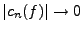 quand
quand
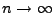 . On sait également que
la série de Fourier de
. On sait également que
la série de Fourier de  converge (fortement) vers
converge (fortement) vers  .
Il est possible de démontrer également la convergence
presque partout (c'est un théorème célèbre de L. Carleson),
mais on n'a pas nécessairement convergence ponctuelle.
.
Il est possible de démontrer également la convergence
presque partout (c'est un théorème célèbre de L. Carleson),
mais on n'a pas nécessairement convergence ponctuelle.
Il est utile de se poser de tels problèmes dans des
cadres fonctionnels différents, par exemple dans le cadre
 .
.
Commençons par le résultat important suivant, appelé
Lemme de Riemann-Lebesgue..
![\begin{theorem}
Soit $f\in L^1([a,b])$, et soit $\alpha\in{\mathbb{R}}$. Alors
\...
...a t}\,dt\longrightarrow 0\hbox{ quand }n\to\infty\ .
\end{equation}\end{theorem}](img92.png)
La démonstration utilise le résultat classique suivant
![\begin{proposition}
$C^1([a,b])$\ est dense dans $L^1([a,b])$.
\end{proposition}](img93.png)
Preuve du Théorème ![[*]](crossref.png) :
Supposons dans un premier temps que
:
Supposons dans un premier temps que
![$ f\in C^1([a,b])$](img94.png) . Alors, par
intégration par parties, on a
. Alors, par
intégration par parties, on a
qui tend bien vers 0 quand
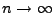 .
On utilise maintenant la densité de
.
On utilise maintenant la densité de
![$ C^1([a,b])$](img96.png) dans
dans
![$ L^1([a,b])$](img97.png) : si
: si
![$ f\in L^1([a,b])$](img98.png) , pour tout
, pour tout
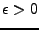 , il existe
, il existe
![$ g_\epsilon \in C^1([a,b])$](img99.png) tel que
tel que
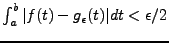 . Alors
. Alors
Pour tout 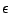 , il existe
, il existe 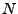 tel que la seconde intégrale soit
plus petite que
tel que la seconde intégrale soit
plus petite que
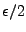 pour
pour 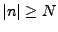 . Ceci complète la
démonstration.
. Ceci complète la
démonstration.

Une conséquence importante de ce résultat est le résultat
suivant de convergence ponctuelle. Pour simplifier, on se
limitera dans cette section au cas particulier 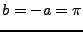 .
Etant donné un point
.
Etant donné un point  , on notera
, on notera
quand ces limites existent.
![\begin{theorem}[Dirichlet]
Soit $f\in L^1_p([-\pi,\pi])$. Soit $t_0$\ un point t...
... \to \frac1{2}\left(f(t_{0+}) + f(t_{0-}) \right)\ .
\end{equation}\end{theorem}](img109.png)
Preuve:
Commençons par évaluer la somme partielle 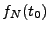 :
:
La même expression appliquée à la fonction constante 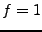 donne
donne
En posant
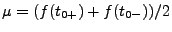 , on a donc
, on a donc
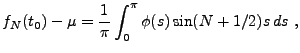 |
(1.6) |
où on a posé
Puisque  est supposée différentiable à droite et à gauche en
est supposée différentiable à droite et à gauche en
 ,
, 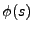 admet une limite finie en
admet une limite finie en 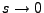 . Donc, il existe
. Donc, il existe
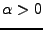 tel que
tel que 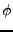 soit bornée sur
soit bornée sur
![$ ]0,\alpha]$](img128.png) :
:
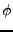 est donc intégrable sur
est donc intégrable sur
![$ ]0,\alpha]$](img128.png) .
Comme
.
Comme
![$ f\in L^1([-\pi,\pi])$](img53.png) ,
, 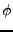 est également intégrable sur
est également intégrable sur
![$ ]\alpha,\pi]$](img130.png) , et donc sur
, et donc sur ![$ [0,\pi]$](img131.png) . Il suffit alors d'appliquer le
théorème de Riemann-Lebesgue à (
. Il suffit alors d'appliquer le
théorème de Riemann-Lebesgue à (![[*]](crossref.png) ) pour conclure.
) pour conclure.

EXEMPLE 1.1 Prenons l'exemple de
![$ f\in L^2_p([-\pi,\pi])$](img132.png)
définie par
![$ f(t)=\chi_{[0,\pi]}(t) -\chi_{[-\pi,0]}(t)$](img133.png)
. Un calcul
immédiat donne

, et
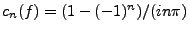
pour
.
On obtient également
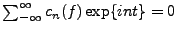
pour
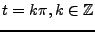
, ce qui coïncide bien avec le résultat
du théorème précédent.
REMARQUE 1.4 En particulier, si de plus

est continue en

,
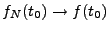
quand
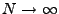
.
REMARQUE 1.5 Il est possible de prouver des versions plus ``fines'' de ce résultat,
ainsi que des résultats de convergence uniforme des séries de Fourier.
On pourra se référer à [
9] pour plus de détails.
Le théorème de Riemann-Lebesgue montre en particulier que si
![$ f\in L^1_p([a,b])$](img141.png) , alors
, alors
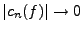 quand
quand
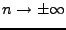 .
En pratique, on s'intéresse non seulement à la convergence
ponctuelle, mais aussi à la vitesse de convergence.
Or cette dernière est directement liée à la régularité de
.
En pratique, on s'intéresse non seulement à la convergence
ponctuelle, mais aussi à la vitesse de convergence.
Or cette dernière est directement liée à la régularité de  ,
comme le montre le lemme suivant.
,
comme le montre le lemme suivant.
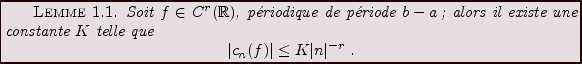
Preuve:
une intégration par parties donne
car  étant continue, on a en particulier
étant continue, on a en particulier 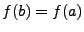 .
Similairement, on a
.
Similairement, on a
Cette dernière intégrale étant bornée par hypothèse,
on en déduit le lemme.

Ceci permet d'estimer la vitesse de convergence des sommes
partielles:
Cependant, on utilise également les séries de Fourier pour
développer des fonctions à support borné. Et il y a là
une différence importante avec le cas des fonctions périodiques.
En effet, le développement en série de Fourier d'une fonction
à support borné n'est pas unique, comme on va le voir.
Soit
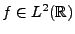 , à support borné dans l'intervalle
, à support borné dans l'intervalle ![$ [a,b]$](img19.png) .
Soit
.
Soit 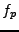 la fonction périodique de période
la fonction périodique de période 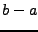 , qui coïncide
avec
, qui coïncide
avec  sur
sur ![$ [a,b]$](img19.png) , définie par
, définie par
Il est clair que
![$ f_p\in L^2_p([a,b])$](img151.png) .
On peut donc la développer en série de
Fourier, et écrire, puisque
.
On peut donc la développer en série de
Fourier, et écrire, puisque
![$ f = f_p \chi_{[a,b]}$](img152.png)
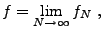 |
(1.7) |
où la limite est toujours à prendre au sens de 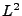 (c'est à dire
(c'est à dire
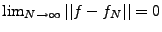 ), et où
), et où
![$\displaystyle f_N(t) = \left(\sum_{n=-N}^N c_n(f) e^{2i\pi nt/(b-a)}\right)\, \chi_{[a,b]}(t)\ ,$](img155.png) |
(1.8) |
et où les coefficients de Fourier
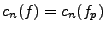 sont toujours
définis par
sont toujours
définis par
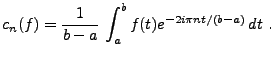 |
(1.9) |
La série de Fourier de la fonction 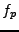 est unique. Cependant, le
passage de
est unique. Cependant, le
passage de  à
à 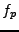 n'est pas la seule possibilité. Il
existe de multiples alternatives, dont on va donner deux exemples ci dessous.
n'est pas la seule possibilité. Il
existe de multiples alternatives, dont on va donner deux exemples ci dessous.
Considérons tout d'abord la fonction 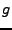 , définie sur l'intervalle
, définie sur l'intervalle
![$ [2a-b,b]$](img158.png) par
par
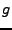 est une fonction symétrique par rapport à
est une fonction symétrique par rapport à 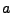 , et on
peut considérer sa périodisée, de période
, et on
peut considérer sa périodisée, de période 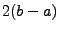
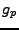 admet un développement en série de Fourier
admet un développement en série de Fourier
où
Cependant, on peut aussi écrire, pour 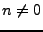 ,
,
et
Posons maintenant
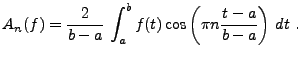 |
(1.10) |
Il est clair que
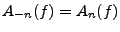 ;
la série de Fourier de
;
la série de Fourier de 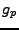 s'écrit maintenant
s'écrit maintenant
Ceci nous donne directement une autre série de Fourier pour la
fonction  :
:
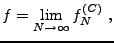 |
(1.11) |
où les sommes partielles 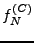 sont définies par
sont définies par
![$\displaystyle f_N^{(C)}(t) = \left(\frac1{2}A_0 +\sum_{n=1}^N A_n(f)\cos\left(\pi n\frac{t-a}{b-a}\right)\right)\chi_{[a,b]}(t)\ .$](img173.png) |
(1.12) |
Une autre possibilité consiste à considérer une extension non
pas symétrique (comme l'est la fonction  ) de
) de  , mais une extension
antisymétrique
, mais une extension
antisymétrique  , définie par
, définie par
Il est alors facile de vérifier que la même procédure
conduit à un développement en série de sinus: on a
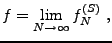 |
(1.13) |
où les sommes partielles 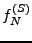 sont définies par
sont définies par
![$\displaystyle f_N^{(S)}(t) = \left(\sum_{n=1}^N B_n(f)\sin\left(\pi n\frac{t-a}{b-a}\right)\right)\chi_{[a,b]}(t)\ ,$](img178.png) |
(1.14) |
et où les coefficients 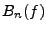 sont donnés par
sont donnés par
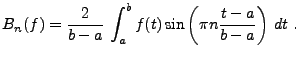 |
(1.15) |
La question qui se pose alors est celle du choix de la série
à utiliser. Dans certaines applications, par exemple pour le codage
des signaux ou des images, on a intérêt à privilégier la
vitesse de décroissance des coefficients du développement de  .
Nous avons vu plus haut que celui-ci est directement lié à la
régularité, non pas de
.
Nous avons vu plus haut que celui-ci est directement lié à la
régularité, non pas de  elle même, mais de la fonction
périodique utilisée dans le développement, c'est à dire
ici
elle même, mais de la fonction
périodique utilisée dans le développement, c'est à dire
ici  , ou
, ou 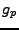 , ou la fonction équivalente dans le
cas du développement en série de sinus.
, ou la fonction équivalente dans le
cas du développement en série de sinus.
Or, même si  est une fonction continue, il est rare qu'elle
soit telle que
est une fonction continue, il est rare qu'elle
soit telle que 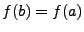 . Donc
. Donc 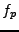 est discontinue, et
les coefficients
est discontinue, et
les coefficients 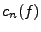 n'ont aucune raison de décroître
assez vite quand
n'ont aucune raison de décroître
assez vite quand 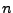 est grand.
Par contre, si
est grand.
Par contre, si  est continue, alors il est facile de voir que
est continue, alors il est facile de voir que
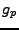 est continue également, de sorte que les coefficients
est continue également, de sorte que les coefficients 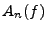 ont toutes les chances de décroître plus rapidement que
les coefficients
ont toutes les chances de décroître plus rapidement que
les coefficients 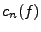 .
.
C'est pourquoi on utilise souvent les séries de cosinus dans
les codeurs de signaux comme ceux employés dans les standards de
communication (comme JPEG ou MPEG par exemple).
EXEMPLE 1.2 Comme illustration de cet fait, prenons la fonction
![$ f(t)=\chi_{[0,\pi]}$](img182.png)
.
Un calcul immédiat montre que
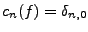
.
Par contre, les coefficients
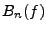
se comportent comme
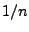
;
Le développement en série de sinus est donc très
inapproprié dans ce cas, comme on peut le voir en
F
IG. ![[*]](crossref.png)
, avec l'approximation par
cosinus (qui est exacte, et identique à la série de Fourier
usuelle, et ne comporte qu'un terme) et l'approximation par une série
de sinus comportant 10 termes. La série de sinus convergera toujours
vers 0 en
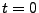
et en
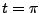
.
Figure:
Diverses séries de Fourier décrivant
![$ \chi_{[0,\pi]}$](img187.png) :
série de sinus, série de cosinus.
:
série de sinus, série de cosinus.
|
|
EXEMPLE 1.3 On considère l'exemple de la fonction
définie sur
![$ [0,\pi]$](img131.png)
. Un calcul explicite montre que ses coefficients
de Fourier sont donnés par
Par contre, on a aussi
et
Donc, dans ce cas particulier, le développement en série de
sinus est le plus économique. Les figures
![[*]](crossref.png)
et
![[*]](crossref.png)
représentent les approximations obtenues
avec ces 3 développements, respectivement

,
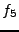
,
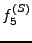
et
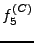
. La figure
![[*]](crossref.png)
représente
l'erreur d'approximation dans les 3 cas:
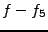
,
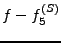
et

.
Figure:
Diverses séries de Fourier décrivant un arc de parabole:
arc de parabole (tirets), et sa série de Fourier usuelle
(trait plein).
|
|
Figure:
Diverses séries de Fourier décrivant un arc de parabole (suite):
série de sinus (tirets) et série de cosinus (trait plein).
|
|
Figure:
Diverses séries de Fourier décrivant un arc de parabole (suite):
erreurs de reconstruction. Série de cosinus (trait plein), de sinus
(tirets et pointillés) et deexponentielles (tirets)
|
|
Etant données deux fonctions périodiques 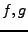 , on leur
associe leur produit de convolution
, on leur
associe leur produit de convolution 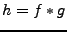 , défini par
, défini par
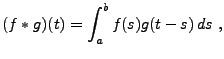 |
(1.16) |
pour tout 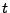 tel que l'intégrale converge.
On a le résultat suivant:
tel que l'intégrale converge.
On a le résultat suivant:
![\begin{proposition}[Young]
Soient $f\in L^p_p([a,b])$\ et $g\in L^q_p([a,b])$, o...
... \le C_{pq}\,\Vert f\Vert _p\,\Vert g\Vert _q\ .
\end{equation}\end{proposition}](img201.png)
Considérons donc
![$ f\in L^2_p([a,b])$](img84.png) , et
, et
![$ h\in L^1_p([a,b])$](img202.png) ;
il résulte des inégalités d'Young que
;
il résulte des inégalités d'Young que
![$ f*h\in L^2_p([a,b])$](img203.png) .
On peut donc calculer
.
On peut donc calculer
Notons que ce résultat reste vrai si on suppose que
![$ h\in L^2_p([a,b])$](img205.png) ,
grâce aux relations d'inclusion que nous avons vues.
,
grâce aux relations d'inclusion que nous avons vues.
D'un autre coté, supposons
![$ f,g\in L^2_p([a,b])$](img206.png) . Alors, d'après
l'inégalité de Cauchy-Schwarz,
. Alors, d'après
l'inégalité de Cauchy-Schwarz,
![$ fg\in L^1_p([a,b])$](img207.png) , et on
peut calculer les coefficients de Fourier
, et on
peut calculer les coefficients de Fourier
On obtient donc un produit de convolution des suites 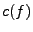 et
et
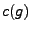 .
.
![\begin{proposition}
Soient $f,g\in L^2_p([a,b])$. Les coefficients de Fourier $c...
...n-m}(g)\\
c_n(f*g) &=& (b-a)\,c_n(f)\,c_n(g)\ .
\end{eqnarray}\end{proposition}](img214.png)
Par définition, on appelle signal numérique (ou digital)
une suite 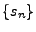 de nombres réels , finie ou infinie.
On considère tout d'abord le cas infini.
Le cadre mathématique le plus couramment utilisé est
le cadre des signaux d'énergie finie
de nombres réels , finie ou infinie.
On considère tout d'abord le cas infini.
Le cadre mathématique le plus couramment utilisé est
le cadre des signaux d'énergie finie
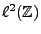 .
.
Les résultats obtenus plus haut (séries de Fourier)
se transposent de façon immédiate au cas des signaux numériques.
En effet, la théorie 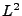 des séries de Fourier permet de
construire une isométrie bijective entre
des séries de Fourier permet de
construire une isométrie bijective entre
![$ L^2_p([-\pi,\pi])$](img216.png) et
et
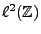 .
La transformation inverse porte le nom de transformation de Fourier
discrète.
.
La transformation inverse porte le nom de transformation de Fourier
discrète.
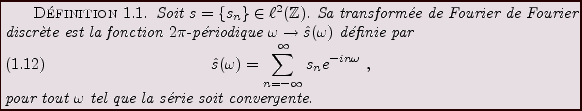
La variable 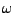 est appelée ``fréquence'' (ou pulsation).
Il résulte de la théorie des séries de Fourier que la TFD
d'une suite de
est appelée ``fréquence'' (ou pulsation).
Il résulte de la théorie des séries de Fourier que la TFD
d'une suite de
 est une fonction
est une fonction  -périodique, de
carré intégrable sur
-périodique, de
carré intégrable sur
![$ [-\pi,\pi]$](img220.png) , et que la transformation inverse
est donnée par le calcul des coefficients de Fourier de
, et que la transformation inverse
est donnée par le calcul des coefficients de Fourier de 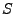 .
Plus précisément, on a
.
Plus précisément, on a

REMARQUE 1.6 On verra plus loin, au moment de décrire la théorie de
l'échantillonnage, l'utilité de cette transformation.
Il est souvent nécessaire d'utiliser une variante, définie par
où
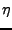
est un réel strictement positif fixé (appelé
fréquence d'échantillonnage).
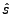
est alors
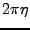
-périodique, et on a également
Les opérations de filtrage sont les opérations de base
du traitement du signal. Le filtrage est utilisé pour
modifier le ``contenu fréquentiel'' des signaux.

Il est immédiat qu'un tel opérateur commute avec les
translations entières: étant donnée
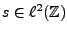 , si on
note
, si on
note 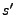 une translatée de
une translatée de 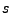 :
:
il vient immédiatement
REMARQUE 1.7 Il est immédiat, d'après les inégalités d'Young, que
si la réponse impulsionnelle
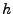
est de module sommable
(i.e.
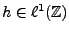
), le filtre
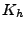
est automatiquement
stable et continu
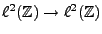
.
La TFD simplifie considérablement les opérations de filtrage
numérique: il est facile de vérifier (par un changement
d'indice de sommation) que si
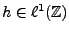 ,
,
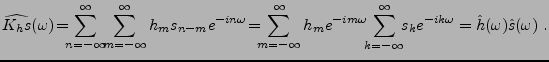 |
(1.17) |
La fonction 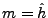 est appelée fonction de transfert
du filtre
est appelée fonction de transfert
du filtre  .
Par conséquent, les filtres numériques sont essentiellement utilisés
pour modifier le contenu fréquentiel des signaux (on en verra des
applications par la suite).
.
Par conséquent, les filtres numériques sont essentiellement utilisés
pour modifier le contenu fréquentiel des signaux (on en verra des
applications par la suite).
Plus généralement, partant d'une fonction de transfert
![$ m\in L^\infty([-\pi,\pi])$](img238.png) , il est facile de voir que l'opérateur
linéaire
, il est facile de voir que l'opérateur
linéaire
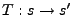 défini par
défini par
est un filtre numérique; sa réponse impulsionnelle est la TFD inverse de
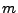 .
.
REMARQUE 1.8 Dans ce cas,
![$ m\in L^\infty([-\pi,\pi])\subset L^2([-\pi,\pi])$](img242.png)
, de
sorte que la réponse impulsionnelle
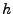
, TFD inverse de
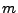
,
appartient automatiquement à
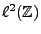
. Par contre, elle n'est
généralement pas dans
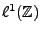
, ce qui peut parfois poser
des problèmes pratiques, comme on va le voir plus loin.
L'exemple le plus simple est celui du
filtre passe-bas idéal, qui force à zéro toutes les fréquences
supérieures (en valeur absolue) à une certaine fréquence
de coupure
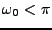 . Un tel filtre est défini par sa fonction
de transfert
. Un tel filtre est défini par sa fonction
de transfert
Après TFD inverse, on obtient la réponse impulsionnelle suivante
Il est facile de voir que la réponse impulsionnelle de ce
filtre n'appartient pas à
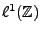 . Plus grave, ce filtre
n'est pas réalisable, et ne peut donc pas être utilisé
de façon exacte en pratique (on est obligé de
tronquer les sommes infinies intervenant dans le calcul).
. Plus grave, ce filtre
n'est pas réalisable, et ne peut donc pas être utilisé
de façon exacte en pratique (on est obligé de
tronquer les sommes infinies intervenant dans le calcul).
Un exemple de filtrage passe-bas utilisant un filtre idéal est
décrit en FIG ![[*]](crossref.png) : un signal (transitoire), et
deux versions filtrées avec des fréquences de coupure différentes.
On voit bien l'effet du filtrage qui atténue fortement les composantes
les plus rapidement variables dans le signal. En particulier, dans le premier
signal filtré (figure du milieu), les composantes très rapidement
variables (donc les très hautes fréquences) ont été supprimées,
mais des oscillations régulières subsistent. Par contre, dans le second
exemple (figure du bas) obtenu avec une fréquence de coupure
: un signal (transitoire), et
deux versions filtrées avec des fréquences de coupure différentes.
On voit bien l'effet du filtrage qui atténue fortement les composantes
les plus rapidement variables dans le signal. En particulier, dans le premier
signal filtré (figure du milieu), les composantes très rapidement
variables (donc les très hautes fréquences) ont été supprimées,
mais des oscillations régulières subsistent. Par contre, dans le second
exemple (figure du bas) obtenu avec une fréquence de coupure
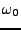 inférieure à la précédente, ces oscillations ont
été supprimées.
inférieure à la précédente, ces oscillations ont
été supprimées.
Figure:
Exemple de filtrage passe-bas: un signal transitoire,
et deux versions filtrées (filtre passe-bas idéal)
avec des fréquences de coupure différentes.
|
|
Les exemples les plus simples de filtres sont les filtres
à réponse impulsionnelle finie (filtres FIR), c'est
à dire tels que la suite 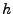 soit de support fini:
soit de support fini:
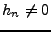 seulement si
seulement si
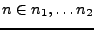 . La fonction
de transfert est alors un polynôme trigonométrique
. La fonction
de transfert est alors un polynôme trigonométrique
L'exemple le plus simple est celui du filtre passe-bas élémentaire,
qui consiste simplement à effectuer des ``moyennes'' locales sur
le signal d'entrée. Ce filtre est défini par
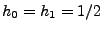 , et
, et
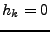 sinon. Il est immédiat de voir que la fonction de transfert
de ce filtre est la fonction
sinon. Il est immédiat de voir que la fonction de transfert
de ce filtre est la fonction
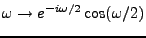 ,
de sorte que
,
de sorte que
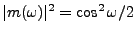 . multiplier la transformée
de Fourier d'un signal par une telle fonction revient à l'atténuer
au voisinage de
. multiplier la transformée
de Fourier d'un signal par une telle fonction revient à l'atténuer
au voisinage de
 , tout en la préservant au voisinage
de
, tout en la préservant au voisinage
de  . C'est le propre d'un filtrage passe-bas, loin d'un filtre
idéal toutefois. De même, le choix
. C'est le propre d'un filtrage passe-bas, loin d'un filtre
idéal toutefois. De même, le choix
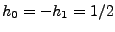 , et
, et
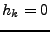 sinon condiot à
sinon condiot à
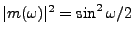 , ce qui
donne un filtre ``passe-haut'', qui atténue les basses fréquences
tout en préservant les hautes fréquences.
, ce qui
donne un filtre ``passe-haut'', qui atténue les basses fréquences
tout en préservant les hautes fréquences.
Les filtres FIR ne sont en général pas suffisants, et il est
nécessaire de recourir à des filtres à réponse impulsionnelle
infinie (filtres IIR). Cependant, il est en pratique
impossible d'implémenter des convolutions discrètes par
des suites de longueur infinie. On a alors recours à une
variante, appelée ``filtrage récursif''.
L'idée de base du filtre récursif est de calculer de façon
itérative une nouvelle valeur du signal filtré par filtrage FIR
des valeurs passées du signal original et du signal filtré.
Cette procédure est donc compatible avec des problématiques
de ``temps réel''. Plus précisément, un filtre
récursif associe à 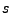 la suite
la suite 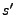 définie par
définie par
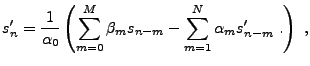 |
(1.18) |
où les coefficients 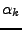 et
et 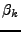 sont des nombres complexes
fixés. Il s'agit donc d'une succession d'opérations causales.
sont des nombres complexes
fixés. Il s'agit donc d'une succession d'opérations causales.
La question est alors de trouver sous quelles conditions
de telles opérations définissent un filtre continu sur
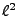 , ou tout du moins un filtre stable. Pour cela, remarquons que
les signaux d'entrée
, ou tout du moins un filtre stable. Pour cela, remarquons que
les signaux d'entrée 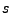 et de sortie
et de sortie 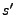 du
filtre sont reliés par une relation du type
du
filtre sont reliés par une relation du type
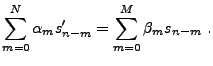 |
(1.19) |
Il est facile de voir qu'après transformation de Fourier
discrète, on aboutit à une relation du type
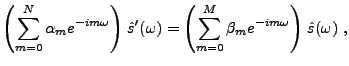 |
(1.20) |
de sorte que la fonction de transfert 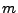 du filtre correspondant
prend la forme d'une fraction rationnelle de deux polynômes
trigonométriques
du filtre correspondant
prend la forme d'une fraction rationnelle de deux polynômes
trigonométriques
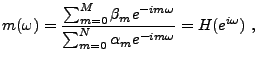 |
(1.21) |
pour une certaine fonction rationnelle  . Les propriétés
du filtre dépendent bien évidemment des propriétés
de
. Les propriétés
du filtre dépendent bien évidemment des propriétés
de 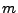 , et en particulier de son dénominateur. On peut facilement voir
que si le dénominateur ne s'annulle pas (c'est à dire si les
racines du dénominateur de la fonction
, et en particulier de son dénominateur. On peut facilement voir
que si le dénominateur ne s'annulle pas (c'est à dire si les
racines du dénominateur de la fonction
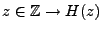 n'appartiennent
pas au cercle unité), la fonction
n'appartiennent
pas au cercle unité), la fonction 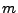 est bornée, et le filtre
correspondant est continu sur
est bornée, et le filtre
correspondant est continu sur
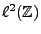 . On a donc
. On a donc

La fonction de transfert 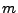 du filtre correspondant est une
fonction périodique, et peut être décomposée en
série de Fourier. Cependant, celle-ci est (sauf dans certains
cas triviaux) une série infinie, de sorte que le filtre
considéré est bel et bien un filtre IIR.
L'expression (
du filtre correspondant est une
fonction périodique, et peut être décomposée en
série de Fourier. Cependant, celle-ci est (sauf dans certains
cas triviaux) une série infinie, de sorte que le filtre
considéré est bel et bien un filtre IIR.
L'expression (![[*]](crossref.png) ) montre donc qu'il est possible d'effectuer
un filtrage IIR en n'utilisant qu'un nombre fini d'opérations. Cette
remarque est d'une importance considérable en pratique.
) montre donc qu'il est possible d'effectuer
un filtrage IIR en n'utilisant qu'un nombre fini d'opérations. Cette
remarque est d'une importance considérable en pratique.
Il est évident que le propriétés du filtre dépendent
fortement des caractéristiques de la fonction de transfert 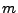 , et
en particulier des zéros de son dénominateur. Ce dernier étant
(tout comme le numérateur) un polynôme trigonométrique,
c'est donc un polynôme dans la variable complexe
, et
en particulier des zéros de son dénominateur. Ce dernier étant
(tout comme le numérateur) un polynôme trigonométrique,
c'est donc un polynôme dans la variable complexe
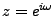 ,
ce qui rend l'étude des zéros plus facile. Les zéros du
numérateur et du dénominateur sont les racines de polynômes
en
,
ce qui rend l'étude des zéros plus facile. Les zéros du
numérateur et du dénominateur sont les racines de polynômes
en 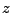 correspondants, ces dernières étant en général
complexes. Ceci suggère d'utiliser des techniques de fonctions
d'une variable complexe, et conduit naturellement à introduire
un outil voisin de la TFD, à savoir la transformation en
correspondants, ces dernières étant en général
complexes. Ceci suggère d'utiliser des techniques de fonctions
d'une variable complexe, et conduit naturellement à introduire
un outil voisin de la TFD, à savoir la transformation en 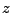 .
.
La transformation en 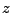 associe à une suite une fonction d'une
variable complexe
associe à une suite une fonction d'une
variable complexe 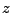 (on pourra se référer
à [1,2,8] pour plus de précision sur
la théorie des fonctions d'une variable complexe).
Elle peut être vue comme un prolongement
de la TFD dans le plan complexe, et ses propriétés en font un
outil très utilisé par les ``signalistes'' (voir
par exemple [4,8]).
Etant donné un signal numérique
(on pourra se référer
à [1,2,8] pour plus de précision sur
la théorie des fonctions d'une variable complexe).
Elle peut être vue comme un prolongement
de la TFD dans le plan complexe, et ses propriétés en font un
outil très utilisé par les ``signalistes'' (voir
par exemple [4,8]).
Etant donné un signal numérique
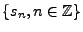 , il existe des cas
où sa transformée de Fourier discrète n'est pas définie au
sens classique. On a parfois recours à une alternative, la
transformée en
, il existe des cas
où sa transformée de Fourier discrète n'est pas définie au
sens classique. On a parfois recours à une alternative, la
transformée en 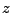 , dont on décrit ci-dessous les propriétés
essentielles, sans entrer dans les détails.
, dont on décrit ci-dessous les propriétés
essentielles, sans entrer dans les détails.
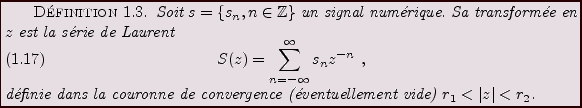
On sait d'après des résultats généraux sur les séries de Laurent que
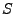 est holomorphe dans sa couronne de convergence.
Inversement, étant donnée une fonction
est holomorphe dans sa couronne de convergence.
Inversement, étant donnée une fonction 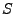 holomorphe dans une
couronne
holomorphe dans une
couronne
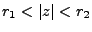 , elle admet un unique développement
en série de Laurent.
De plus, on a le lemme
classique suivant:
, elle admet un unique développement
en série de Laurent.
De plus, on a le lemme
classique suivant:

On en déduit immédiatement la couronne de convergence de
la transformée en 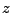 d'un signal numérique:
d'un signal numérique:

EXEMPLE 1.4 On dit qu'un signal numérique
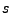
est
causal si
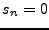
pour tout
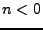
. Inversement,
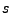
est dit
anticausal si
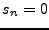
pour tout
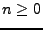
. Supposons que
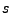
soit causal. Alors
il est évident que
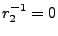
, de sorte que la transformée en
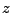
de
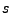
est bien définie dans le domaine
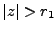
,
c'est à dire à l'extérieur d'un cercle de rayon
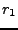
.
De même, si 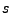 est anticausal,
est anticausal, 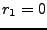 , et
, et 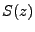 est bien défini
à l'intérieur du cercle de rayon
est bien défini
à l'intérieur du cercle de rayon 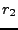 .
.
Il existe plusieurs techniques permettant d'inverser une transformation
en 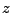 . La plus simple consiste à expliciter un développement
en série de Laurent de la fonction
. La plus simple consiste à expliciter un développement
en série de Laurent de la fonction 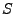 considérée. Le
développement en série de Laurent étant unique, ceci
fournit directement une transformée inverse.
considérée. Le
développement en série de Laurent étant unique, ceci
fournit directement une transformée inverse.
EXEMPLE 1.5 Prenons l'exemple de la fonction
on peut alors écrire, pour
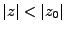
,
ce qui, conjugué à l'unicité du développement en
série de Laurent, fournit
Une alternative consiste à utiliser la TFD. Soit 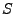 la transformée
en
la transformée
en 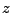 d'un signal
d'un signal 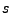 , et soit
, et soit 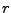 un nombre tel que
un nombre tel que 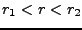 .
Calculons
.
Calculons
On peut donc écrire
Par un changement de variables complexes
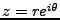 ,
on obtient donc
,
on obtient donc
![\begin{proposition}
Soit $s$\ un signal num\'erique, et soit $S$\ sa transform\'...
...\'e sur l'origine du plan complexe,
de rayon $r\in ]r_1,r_2[$.
\end{proposition}](img294.png)
On a généralement recours à la méthode des résidus
pour calculer de telles intégrales.
L'un des intérêts de la transformation en 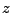 est son comportement
vis à vis des transformations simples, et en particulier des
translations. Etant donnée une suite
est son comportement
vis à vis des transformations simples, et en particulier des
translations. Etant donnée une suite
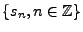 , et une suite
filtres
, et une suite
filtres
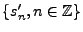 donnée par
donnée par
 , on voit immédiatement que leurs transformées
en
, on voit immédiatement que leurs transformées
en 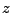 sont reliées par
sont reliées par
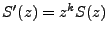 .
Le corollaire immédiat est le comportement de la
transformation en
.
Le corollaire immédiat est le comportement de la
transformation en 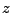 vis à vis du filtrage numérique.
Etant donné un signal numérique
vis à vis du filtrage numérique.
Etant donné un signal numérique 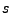 et une filtre numérique
de réponse impulsionnelle
et une filtre numérique
de réponse impulsionnelle 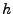 , alors pour tout
, alors pour tout 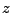 à
l'intérieur de l'intersection des couronnes de convergence des
transformées
à
l'intérieur de l'intersection des couronnes de convergence des
transformées 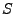 et
et  de
de 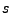 et
et 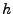 respectivement, on a
respectivement, on a
de sorte que l'on a
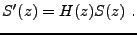 |
(1.22) |
La fonction  est elle aussi appelée fonction de transfert
du filtre.
est elle aussi appelée fonction de transfert
du filtre.
En particulier, dans le cas d'un filtre récursif
comme précédemment, on a
c'est à dire que la transformée en 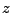 de
de 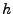 prend la forme
d'une fraction rationnelle. Cette expression est à rapprocher
de l'expression (
prend la forme
d'une fraction rationnelle. Cette expression est à rapprocher
de l'expression (![[*]](crossref.png) ) obtenue avec la TFD.
) obtenue avec la TFD.
On dit qu'un filtre causal 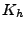 est d'ordre fini si
est d'ordre fini si 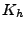 peut être
réalisé comme un filtre récursif comme en (
peut être
réalisé comme un filtre récursif comme en (![[*]](crossref.png) ).
On impose que le filtre
).
On impose que le filtre 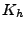 soit causal (donc la couronne de convergence
de
soit causal (donc la couronne de convergence
de 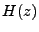 est de la forme
est de la forme 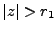 ) et stable (donc le cercle unité
est inclus dans la couronne de convergence). Par conséquent, les
pôles de
) et stable (donc le cercle unité
est inclus dans la couronne de convergence). Par conséquent, les
pôles de  se trouvent à l'intérieur du cercle unité.
se trouvent à l'intérieur du cercle unité.
On se limite ici aux filtres réels, c'est à dire tels que
les coefficients 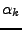 et
et 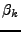 sont réels.
Dans ce cas, il est facile de voir que
sont réels.
Dans ce cas, il est facile de voir que
de sorte que le spectre prend la forme
Notons 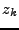 les pôles de
les pôles de  (les zéros du dénominateur de
(les zéros du dénominateur de  )
et
)
et
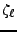 les zéros de
les zéros de  . Il est immédiat que
. Il est immédiat que
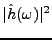 est caractérisé par des facteurs de la forme
est caractérisé par des facteurs de la forme
(avec
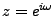 ), et est donc une fonction (positive rationnelle) de
), et est donc une fonction (positive rationnelle) de
Inversement, soit
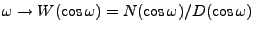 une fonction rationnelle positive. Notons
une fonction rationnelle positive. Notons
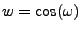 , et
, et 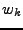 les zéros (dans le plan complexe) de
les zéros (dans le plan complexe) de 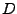 (le numérateur
(le numérateur 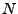 se traite de façon identique). On voit facilement que l'équation
en
se traite de façon identique). On voit facilement que l'équation
en 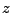
possède deux solutions inverses l'une de l'autre, notées
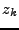 et
et
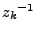 . Par convention, on choisit
. Par convention, on choisit 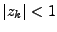 .
On peut alors poser
.
On peut alors poser
De même, en notant 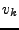 les zéros de
les zéros de 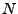 , et
, et 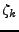 et
et
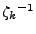 les solutions et
les solutions et 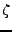 de
de
(sans nécessairement imposer
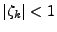 ), on est naturellement conduit
à introduire
), on est naturellement conduit
à introduire
Il résulte de cette analyse que la fonction
est la fonction de transfert d'un filtre causal stable d'ordre fini.

REMARQUE 1.9 Le filtre
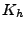
n'est pas unique, car il reste la liberté de
choisir les zéros
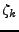
à l'intérieur ou à l'extérieur
du disque unité pour former la fonction
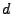
. Choisir tous les zéros
à l'intérieur du disque unité conduit aux filtres dits
à phase minimale.
Un exemple est donné par la famille des filtres de Butterworth
(dans leur version numérique), qui constituent des approximations
de filtres passe-bas idéaux. En introduisant de nouveau la variable
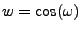 , les filtres de Butterworth sont caractérisés par
une fonction de transfert telle que
, les filtres de Butterworth sont caractérisés par
une fonction de transfert telle que
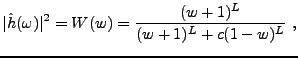 |
(1.23) |
où 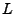 est un nombre entier fixé, et
est un nombre entier fixé, et 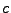 une constante positive.
Un exemple d'une telle fonction
une constante positive.
Un exemple d'une telle fonction 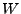 se trouve en FIG
se trouve en FIG ![[*]](crossref.png)
Figure:
Module de la fonction de transfert
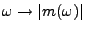 (en logarithme) pour un filtre de Butterworth numérique d'ordre
(en logarithme) pour un filtre de Butterworth numérique d'ordre 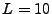 ,
avec une fréquence de coupure
,
avec une fréquence de coupure
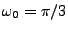 ).
).
|
|
Il est facile de vérifier qu'une telle fonction 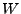 entre tout
à fait dans les hypothèses de la Proposition
entre tout
à fait dans les hypothèses de la Proposition ![[*]](crossref.png) . Par
conséquent, il est toujours possible de trouver un filtre causal
d'ordre fini, de réponse impulsionnelle
. Par
conséquent, il est toujours possible de trouver un filtre causal
d'ordre fini, de réponse impulsionnelle 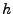 , tel que
l'équation (
, tel que
l'équation (![[*]](crossref.png) ) soit satisfaite.
) soit satisfaite.
Le nombre 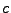 contrôle en fait la fréquence de coupure, via la relation
contrôle en fait la fréquence de coupure, via la relation
(par exemple, 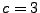 correspond à une fréquence de coupure égale à
correspond à une fréquence de coupure égale à
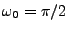 ).
).
Figure:
Position dans le plan complexe des 10 pôles de la fonction
de transfert 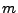 pour un filtre de Butterworth d'ordre 10, pour
une fréquence de coupure égale à
pour un filtre de Butterworth d'ordre 10, pour
une fréquence de coupure égale à 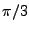 .
.
|
|
Par exemple, dans le cas 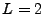 , on peut montrer que les (deux) racines
complexes du dénominateur de la fonction de transfert
, on peut montrer que les (deux) racines
complexes du dénominateur de la fonction de transfert  sont de la forme
sont de la forme
(et sont donc complexes conjugués l'un de l'autre).
On a représenté dans la FIG ![[*]](crossref.png) les positions des pôles, c'est à dire des racines du
dénominateur (croix) et des zéros (cercles) de
les positions des pôles, c'est à dire des racines du
dénominateur (croix) et des zéros (cercles) de  pour
pour
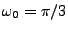 . Comme on
peut le voir, les pôles sont bien à l'intérieur du disque unité.
. Comme on
peut le voir, les pôles sont bien à l'intérieur du disque unité.
On peut similairement obtenir des filtres de Butterworth
passe-bande, par exemple des filtres
sélectionnant une bande de fréquences donnée.
Figure:
Module de la fonction de transfert
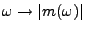 (en logarithme) pour un filtre de passe-bande de Butterworth
numérique d'ordre
(en logarithme) pour un filtre de passe-bande de Butterworth
numérique d'ordre 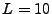 , sélectionnant une bande de fréquence
entre
, sélectionnant une bande de fréquence
entre 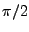 et
et 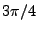 .
.
|
|
Figure:
Position dans le plan complexe des 2 zéros (d'ordre 5 chacun)
et des 10 pôles de la fonction
de transfert 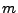 pour un filtre passe-bande de Butterworth d'ordre 10,
sélectionnant une bande de fréquences entre
pour un filtre passe-bande de Butterworth d'ordre 10,
sélectionnant une bande de fréquences entre 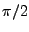 et
et 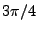 .
.
|
|
Le problème de détection optimale est un problème classique
du traitement du signal. On suppose que l'on a un signal de référence
connu
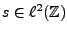 , et que l'on observe un signal
, et que l'on observe un signal 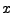 de la forme
de la forme
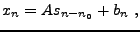 |
(1.24) |
où
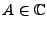 et
et
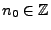 sont inconnus et à déterminer, et
où
sont inconnus et à déterminer, et
où
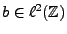 est une perturbation (bruit, ou erreur de mesure), dont
seul est connu le ``spectre''
est une perturbation (bruit, ou erreur de mesure), dont
seul est connu le ``spectre''
Le problème est d'identifier 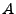 et
et 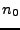 à partir de
à partir de 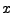 ,
en utilisant des méthodes linéaires.
,
en utilisant des méthodes linéaires.
Pour cela, on considère une famille paramétrique de formes linéaires
sur
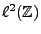 , notées
, notées
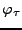 ,
,
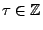 , qui sont donc
de la forme
, qui sont donc
de la forme
 |
(1.25) |
pour une certaine fonction
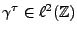 . On peut donc écrire
. On peut donc écrire
On a ici introduit l'opérateur de translation 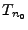 , défini par
, défini par
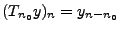 . On cherche alors à trouver la famille de
fonctions
. On cherche alors à trouver la famille de
fonctions
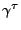 , telle que pour tout
, telle que pour tout 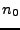 ,
,
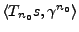 soit le plus grand possible
(en module), tout en gardant le second terme (contribution du bruit)
le plus petit possible.
soit le plus grand possible
(en module), tout en gardant le second terme (contribution du bruit)
le plus petit possible.
Pour cela, calculons
de sorte que l'inégalité de Cauchy-Schwarz donne immédiatement
Le second facteur donne en fait une estimation de la ``taille''
du bruit après calcul de
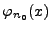 . On peut écrire
. On peut écrire
Cette inégalité est une égalité si et seulement si les deux
facteurs sont proportionnels, c'est à dire si
pour une certaine constante 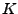 , en d'autres termes, en supposant
que la fonction
, en d'autres termes, en supposant
que la fonction
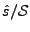 soit bornée,
soit bornée,
Donc, la famille de formes optimale (au sens de l'inégalité
de Cauchy-Schwarz)
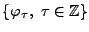 est
définie par
est
définie par
ce qui définit un filtre numérique, de fonction de transfert
On peut donc énoncer le résultat suivant.
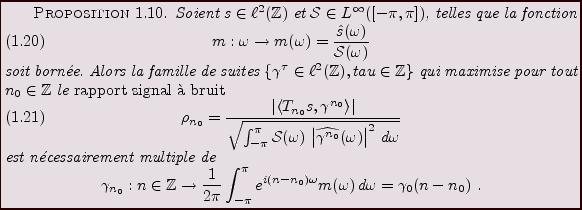
Ainsi, la famille de transformations
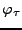 correspondante prend la
forme d'un filtre numérique, de fonction de transfert
correspondante prend la
forme d'un filtre numérique, de fonction de transfert 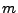 :
:
Finalement, on montre aussi facilement que pour tout
 ,
,
Ceci qui suggère, en présence d'une observation de
la forme (![[*]](crossref.png) ) avec un
) avec un 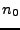 inconnu,
de rechercher les maxima de
inconnu,
de rechercher les maxima de
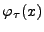 pour estimer
pour estimer 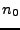 .
Une fois
.
Une fois 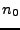 estimé, on peut alors obtenir une estimation
de l'amplitude inconnue
estimé, on peut alors obtenir une estimation
de l'amplitude inconnue 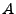 .
.
Un exemple de filtrage adapté est donné en
figure ![[*]](crossref.png) . Comme on le voit, le signal de
sortie du filtre adapté présente un ``pic'', c'est à dire
un maximum bien marqué à la position où le signal de départ
décalé était présent.
. Comme on le voit, le signal de
sortie du filtre adapté présente un ``pic'', c'est à dire
un maximum bien marqué à la position où le signal de départ
décalé était présent.
Figure:
Exemple de filtrage adapté. En haut, le signal original,
au milieu le signal original bruité, en bas le signal de sortie du
filtre adapté, qui présente un maximum bien marqué à la position
du signal original.
|
|
La transformation de Fourier en pratique:
transformation de Fourier finie (TFF)
Les suites de longueur finie se prêtent au même type
d'analyse que les suites infinies. On peut
également leur associer une transformée de Fourier
(qui est elle aussi une suite de longueur finie),
et la transformation correspondante est de nouveau une
isométrie (à une constante près). Plus précisément,
à la suite finie
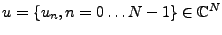 on associe la suite
on associe la suite
 , définie par
, définie par
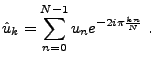 |
(1.26) |
C'est alors un jeu d'enfant que de montrer des propriétés
analogues aux propriétés que nous avons déjà vues:
formule de Parseval et inversion. De fait, on a
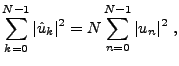 |
(1.27) |
et
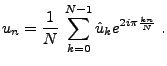 |
(1.28) |
REMARQUE 1.10 En d'autres termes, ceci est
équivalent à dire que la famille des vecteurs
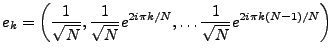 |
(1.29) |
est une base orthonormée de
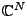
, et un a posé
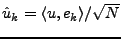
.
La relation plus précise entre la TFD et la TFF peut également
se comprendre de la façon suivante, dans le cas des signaux
de longueur finie.

Preuve:
La preuve résulte de la définition de la TFD, de l'expression des
nombres 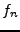 à partir des
à partir des 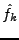 et de la somme de la
série géométrique.
et de la somme de la
série géométrique.

Dans le cas où le signal considéré 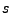 n'est pas à support
fini, il est néanmoins facile d'obtenir une estimation de sa
transformée de Fourier à partir d'un ``segment'' fini, et des
estimations d'erreur grâce à la formule de Parseval.
n'est pas à support
fini, il est néanmoins facile d'obtenir une estimation de sa
transformée de Fourier à partir d'un ``segment'' fini, et des
estimations d'erreur grâce à la formule de Parseval.
Nous nous sommes jusqu'à présent limités au cas des
signaux unidimensionnels, en prenant principalement comme
``inspiration'' les signaux sonores. On a souvent à traiter
des signaux de dimension supérieure, comme par exemple
des images (dimension 2), des vidéos (dimension 2+1) ou même
des signaux en bien plus grande dimension.
Un signal numérique 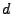 -dimensionnel est défini comme
une suite à
-dimensionnel est défini comme
une suite à 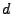 indices
indices
Un exemple de signal bidimensionnel (image) est présenté
en FIG. ![[*]](crossref.png) . L'axe horizontal est l'axe
. L'axe horizontal est l'axe 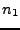 , et l'axe
vertical est l'axe
, et l'axe
vertical est l'axe 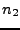 . Un point
. Un point 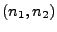 est appelé
pixel. La valeur de l'image
est appelé
pixel. La valeur de l'image
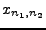 au pixel
au pixel
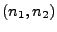 est représentée par un niveau de gris d'intensité
proportionnelle à
est représentée par un niveau de gris d'intensité
proportionnelle à
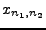 .
.
Figure:
Exemple d'images, en niveaux de gris
|
|
Comme dans le cas unidimensionnel, le modèle le plus classique
est le modèle Hilbertien
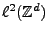 , c'est à dire celui des signaux
dits d'énergie finie, tels que
, c'est à dire celui des signaux
dits d'énergie finie, tels que
Une bonne part des techniques que nous avons vues jusqu'à présent
se transposent aisément au cadre multidimensionnel, en particulier
les outils liés à l'analyse de Fourier.

La TFD 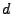 -dimensionnelle possède des propriétés en tous
points similaires à celles de son analogue unidimensionnelle.
En particulier, on voit facilement que
-dimensionnelle possède des propriétés en tous
points similaires à celles de son analogue unidimensionnelle.
En particulier, on voit facilement que 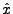 est bien définie
dès que
est bien définie
dès que
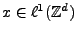 . De même, la théorie
. De même, la théorie 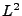 se
transpose facilement
se
transpose facilement

REMARQUE 1.11 La transformée de Fourier discrète
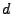
-dimensionnelle d'un signal
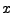
est cette fois une fonction de
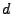
variables fréquentielles.
Dans les cas
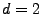
ou
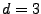
, on parle de fréquence
spatiale
.
Pour fixer les idées, prenons le cas 2D. La représentation de Fourier
représente un signal comme combinaison linéaire de sinusoïdes,
oscillant à la fréquence 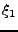 dans la direction 1, et
dans la direction 1, et 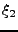 dans
la direction 2. Comme dans le cas 1D, plus la fréquence est élevée,
plus les oscillations sont rapides.
dans
la direction 2. Comme dans le cas 1D, plus la fréquence est élevée,
plus les oscillations sont rapides.
Le filtrage linéaire, que nous avons longuement étudiée dans
le cas unidimensionnel, est l'opération fondamentale du traitement
du signal. Il se généralise presque mot pour mot au cadre
multidimensionnel.
Etant donnée une suite à 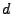 indices
indices 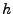 , le filtre linéaire
, le filtre linéaire
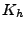 de réponse impulsionnelle
de réponse impulsionnelle 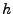 est l'opérateur linéaire
qui associe à tout signal numérique
est l'opérateur linéaire
qui associe à tout signal numérique 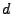 -dimensionnel
-dimensionnel 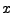 le signal
le signal 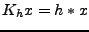 défini par
défini par
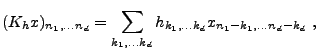 |
(1.30) |
pour tout  -uplet
-uplet
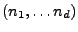 tel que la série converge. De nouveau
il est clair que si
tel que la série converge. De nouveau
il est clair que si
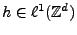 ,
, 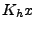 est borné dès que
est borné dès que 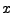 l'est, et
l'est, et
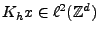 dès que
dès que
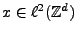 .
.
Le lien avec la TFD est le même que dans le cas unidimensionnel. Supposant
pour simplifier
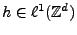 , on montre facilement que
, on montre facilement que
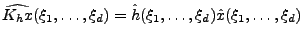 |
(1.31) |
de sorte que l'on peut exprimer le filtrage sous la forme
![$\displaystyle (K_h x)_{n_1,\dots n_d} = \frac1{(2\pi)^d}\int_{[-\pi,\pi]^d} m(\...
...at x(\xi_1,\dots,\xi_d) e^{i(n_1\xi_1 +\dots +n_d\xi_d)}\,d\xi_1\dots d\xi_d\ .$](img413.png) |
(1.32) |
Exemples de filtres bidimensionnels:
Pour illustrer ce que nous venons de voir, considérons le cas bidimensionnel.
- L'exemple le plus simple est celui du filtrage passe-bas idéal, que
l'on peut cette fois concevoir de deux façons différentes:
- Filtrage ``passe haut'' idéal. En définissant la fonction de
transfert comme
où 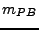 est l'une des deux fonctions de transfert de filtres passe-bas
vue ci-dessus, on obtient un filtre passe haut, qui ne conserve dans les images
que les composantes rapidement variables.
est l'une des deux fonctions de transfert de filtres passe-bas
vue ci-dessus, on obtient un filtre passe haut, qui ne conserve dans les images
que les composantes rapidement variables.
- Filtres tensoriels: la technique du produit tensoriel permet de générer
des filtres 2D à partir de filtres 1D. Soient
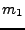 et
et 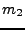 les fonctions
de transfert de deux filtres 1D. On leur associe alors la fonction de transfert
d'un filtre 2D comme suit:
les fonctions
de transfert de deux filtres 1D. On leur associe alors la fonction de transfert
d'un filtre 2D comme suit:
On vérifie facilement que si 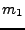 et
et 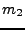 sont des fonctions de
transfert de filtres passe bas,
sont des fonctions de
transfert de filtres passe bas, 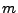 définit aussi un filtre passe-bas.
On peut de cette façon construire de multiples types de filtres.
définit aussi un filtre passe-bas.
On peut de cette façon construire de multiples types de filtres.
Figure:
Image de la Figure ![[*]](crossref.png) , filtrée par filtrage passe-bas.
, filtrée par filtrage passe-bas.
|
|
Nous nous sommes jusqu'à présent focalisés sur deux façons
différentes de ``représenter'' des signaux numériques: la
représentation temporelle (ou spatiale, dans les cas 2D ou 3D), où
un signal est représenté par ses valeurs 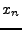 , et la représentation
fréquentielle, dans le domaine de la TFD.
, et la représentation
fréquentielle, dans le domaine de la TFD.
Dans de nombreux domaines, on utilise maintenant d'autres types de
représentations des signaux, exploitant l'analyse fonctionnelle
élémentaire. L'idée est d'utiliser une modélisation des
signaux comme éléments d'un espace de Hilbert (séparable), et
les représenter par les coefficients de leur développement sur
une base bien choisie.
Les notions essentielles pour cette section sont rappelées
dans l'Appendice ![[*]](crossref.png) .
On se focalise ici sur les bases orthonormales,
et on donne quelques exemples de bases ``classiques''.
.
On se focalise ici sur les bases orthonormales,
et on donne quelques exemples de bases ``classiques''.
- Le cas
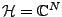 (ou
(ou
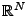 ). On a vu dans la section
). On a vu dans la section ![[*]](crossref.png) que les sinusoïdes
que les sinusoïdes
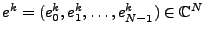 , où
, où
forment une base orthonormée de
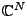 . Ces bases sont en fait peu
utilisées en pratique, car les signaux sont souvent à valeurs réelles,
et on préfère alors éviter de manipuler des nombres complexes.
. Ces bases sont en fait peu
utilisées en pratique, car les signaux sont souvent à valeurs réelles,
et on préfère alors éviter de manipuler des nombres complexes.
On leur préfère alors les bases de
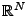 appelées bases
DCT (pour Discrete Cosine Transform). Ces dernières
existent en huit versions différentes, les deux plus ``populaires''
étant:
appelées bases
DCT (pour Discrete Cosine Transform). Ces dernières
existent en huit versions différentes, les deux plus ``populaires''
étant:
- La DCT-II, définie par
- La DCT-IV, définie par
- Bases ``composites'' de
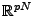 . Lorsque l'on doit représenter
un long signal, par exemple une seconde de son (ce qui représente
habituellement 44100 valeurs par seconde), on ne peut pas se permettre
de travailler dans des espaces vectoriels de si grande dimension, et
on les ``coupe en morceaux'' de la façon suivante.
. Lorsque l'on doit représenter
un long signal, par exemple une seconde de son (ce qui représente
habituellement 44100 valeurs par seconde), on ne peut pas se permettre
de travailler dans des espaces vectoriels de si grande dimension, et
on les ``coupe en morceaux'' de la façon suivante.
Supposons que
 , où
, où 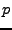 est un entier positif fixé.
Le découpage consiste à écrire
est un entier positif fixé.
Le découpage consiste à écrire
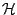 sous la forme de somme
directe
sous la forme de somme
directe
en d'autres termes représenter un signal
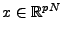 par
par
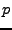 signaux de longueur
signaux de longueur 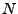 . Ces derniers peuvent ensuite être
représentés par leurs coefficients sur une base usuelle de
. Ces derniers peuvent ensuite être
représentés par leurs coefficients sur une base usuelle de
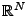 .
.
Plus concrètement, soit
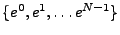 une base orthonormale
de
une base orthonormale
de
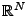 . Pour tout
. Pour tout
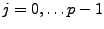 , soit
, soit 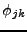 la copie du vecteur
la copie du vecteur
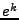 définie par décalage de
définie par décalage de 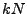 :
:
où 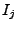 est l'intervalle dans
est l'intervalle dans
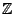
On a alors, pour tout
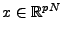
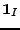 étant l'indicatrice d'un segment
étant l'indicatrice d'un segment 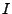 , et on montre facilement que
, et on montre facilement que
de sorte que
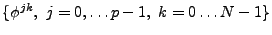 est une base
orthonormée de
est une base
orthonormée de
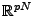 .
.
- Bases de
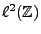 : la base (orthonormale) de
: la base (orthonormale) de
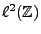 la plus ``commune'' est
la base de Krönecker
la plus ``commune'' est
la base de Krönecker
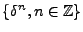 , définie par
, définie par
Cette base n'est toutefois pas très pratique dans de nombreuses situations.
- Dans
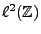 , les fonctions exponentielles complexes intervenant dans
les décompositions de Fourier des signaux numériques ne forment
pas une base de
, les fonctions exponentielles complexes intervenant dans
les décompositions de Fourier des signaux numériques ne forment
pas une base de
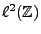 . En effet, ces fonctions ne sont pas elles mêmes
de module carré sommable.
. En effet, ces fonctions ne sont pas elles mêmes
de module carré sommable.
- Pour obtenir des bases trigonométriques de
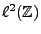 , il faut ``localiser''
ces fonctions, comme on l'a fait ci-dessus dans le cas de
, il faut ``localiser''
ces fonctions, comme on l'a fait ci-dessus dans le cas de
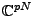 .
En considérant comme précédemment une base orthonormale
.
En considérant comme précédemment une base orthonormale
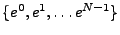 de
de
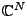 , et en définissant pour tout
, et en définissant pour tout
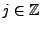 et
et
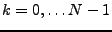 la suite
la suite 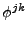 par
par
on montre dans ce cas encore que la famille
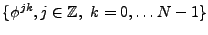 est une base orthonormée
de
est une base orthonormée
de
Il existe de nombreuses situations dans lesquelles les bases orthonormales
que l'on sait construire ne sont pas bien adaptées aux traitements
que l'on voudrait effectuer sur les signaux. En effet, les hypothèses
d'orthonormalité sont souvent trop contraignantes, et ne permettent
pas de générer des familles de signaux élémentaires
sur lesquelles décomposer les signaux, qui possèdent les
propriétés requises.
On peut alors avoir avantage à recourir à la notion de repère,
décrite dans l'Annexe ![[*]](crossref.png) . En quelques mots, les repères
constituent une généralisation de la notion de famille génératrice
de vecteurs, adaptable aux espaces de Hilbert de dimension infinie. Un
repère dans un espace de Hilbert
. En quelques mots, les repères
constituent une généralisation de la notion de famille génératrice
de vecteurs, adaptable aux espaces de Hilbert de dimension infinie. Un
repère dans un espace de Hilbert
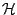 est une famille de vecteurs
est une famille de vecteurs
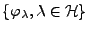 telle qu'il existe deux
constantes strictement positives
telle qu'il existe deux
constantes strictement positives
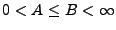 vérifiant,
pour tout
vérifiant,
pour tout
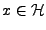 ,
,
On montre facilement (voir l'Annexe ![[*]](crossref.png) ) que dans ces conditions,
l'opérateur d'analyse
) que dans ces conditions,
l'opérateur d'analyse
est borné, et que son adjoint, l'opérateur de synthèse
l'est également, de sorte que l'opérateur de repère
est borné, inversible à inverse borné.
De tels repères peuvent être utilisés pour représenter
des signaux.
EXEMPLE 1.6 Repères de Gabor: Dans
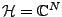
: soit
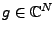
, tel que
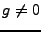
un signal de référence, normalisé de sorte que
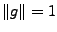
. On lui associe la famille d'
atomes de Gabor, copies
translatées et modulées de
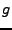
, définies par
où
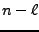
est à prendre mpodulo
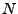
pour que ceci ait un sens.
On vérifie facilement que pour tout
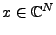 , on a une formule
de type ``formule de Parseval''
, on a une formule
de type ``formule de Parseval''
de sorte que la famille
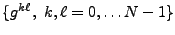
est un repère strict de
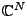
.
Par conséquent, on peut donc écrire tout
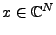 sous la forme
sous la forme
où les coefficients
forment la transformée de Gabor de
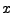
, aussi appelée transformée
de Fourier à court terme de
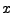
. Notons qu'il s'agit de la transformée
de Fourier de
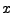
, multipliée par une copie translatée de
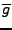
.
Ainsi, si
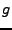
est localisée autour de
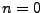
,
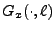
représente une transformée de Fourier d'une copie de
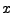
, que l'on a
``localisée'' au voisinage de
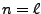
.
EXEMPLE 1.7 Il est possible de développer une version de la transformation de Gabor
adaptée aux signaux numériques infinis
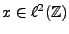
. Elle est cependant
un peu plus complexe.
Bruno Torresani
2007-06-26
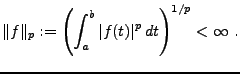
![]() . On dira que
. On dira que
![]() si la restriction de
si la restriction de
![]() à l'intervalle
à l'intervalle ![]() appartient à
appartient à
![]() , et si
, et si ![]() est
périodique dans le sens suivant: en posant
est
périodique dans le sens suivant: en posant ![]() , et
, et
![]() ,
on a
,
on a ![]() pour tout
pour tout ![]() .
.
![]() .
.
![]() appartient à
appartient à
![]() si
si
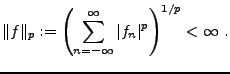
![]() et
et
![]() possèdent des propriétés
simples d'inclusion:
possèdent des propriétés
simples d'inclusion:
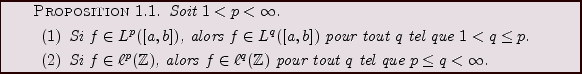
![]() , et soit
, et soit ![]() l'ensemble des points
l'ensemble des points ![]() tels
que
tels
que
![]() . Sur
. Sur ![]() , on a alors
, on a alors
![]() pour
tout
pour
tout ![]() . On a alors, en notant
. On a alors, en notant ![]() ,
,
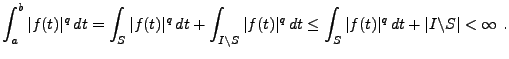
![]() ) et des fonctions (
) et des fonctions (
![]() );
on utilisera régulièrement le résultat suivant
);
on utilisera régulièrement le résultat suivant
![\begin{proposition}[H\uml older]
\index{In \'egalit\'e de H\ölder}
Soient $1\le ...
...g\Vert _r\le \Vert f\Vert _p\,\Vert g\Vert _q\ .
\end{equation}\end{proposition}](img42.png)
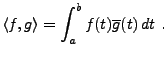
![]() dans
dans
![]() . On peut alors utiliser
le résultat d'approximation des fonctions
continues par des polynômes trigonométriques (voir [7])
pour une démonstration):
. On peut alors utiliser
le résultat d'approximation des fonctions
continues par des polynômes trigonométriques (voir [7])
pour une démonstration):
![\begin{proposition}[Weierstrass]
Soit $f\in C([a,b])$. Pour tout $\epsilon >0$, ...
...in{equation}
\vert f(t) -P(t)\vert\le\epsilon\ .
\end{equation}\end{proposition}](img51.png)
![]() (le cas général
se traite de façon similaire).
Soit
(le cas général
se traite de façon similaire).
Soit
![]() , et supposons que
, et supposons que ![]() soit orthogonale
à toutes les fonctions
soit orthogonale
à toutes les fonctions ![]() :
:
![]() ,
,
![]() .
Soit
.
Soit ![]() définie par
définie par
![]() .
. ![]() est continue par construction,
et vérifie
est continue par construction,
et vérifie ![]() .
Si
.
Si ![]() est une constante
complexe quelconque, une intégration par parties montre que
est une constante
complexe quelconque, une intégration par parties montre que
![]() ,
,
![]() . Un choix adéquat de
. Un choix adéquat de
![]() permet à cette égalité d'être valide pour
permet à cette égalité d'être valide pour ![]() également.
On pose alors
également.
On pose alors
![]() .
.
![]() , et on sait
d'après le résultat ci-dessus que pour tout
, et on sait
d'après le résultat ci-dessus que pour tout
![]() , il existe
un polynôme trigonométrique
, il existe
un polynôme trigonométrique ![]() tel que pour tout
tel que pour tout
![]() ,
,
![]() . Donc, on a
. Donc, on a

![]() , on pose
, on pose
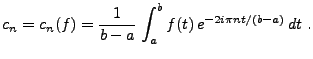
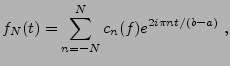
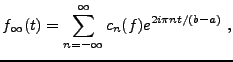
![[*]](crossref.png) de l'Appendice
de l'Appendice ![[*]](crossref.png) )
que si
)
que si
![]() , la suite
, la suite
![]() appartient à
appartient à
![]() , et la série de Fourier
, et la série de Fourier
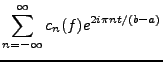

![]() .
.
![\begin{theorem}
Soit $f\in L^1([a,b])$, et soit $\alpha\in{\mathbb{R}}$. Alors
\...
...a t}\,dt\longrightarrow 0\hbox{ quand }n\to\infty\ .
\end{equation}\end{theorem}](img92.png)
![]()
![[*]](crossref.png) :
Supposons dans un premier temps que
:
Supposons dans un premier temps que
![]() . Alors, par
intégration par parties, on a
. Alors, par
intégration par parties, on a
![$\displaystyle \int_a^b f(t) e^{-in\alpha t}\,dt= -\frac1{in\alpha}
[f(b)e^{-in\...
...f(a)e^{-in\alpha a}] +
\frac1{in\alpha}\int_{a}^b f'(t) e^{-in\alpha t}\,dt\ ,
$](img95.png)
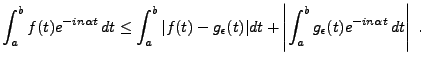
![]() .
Etant donné un point
.
Etant donné un point ![]() , on notera
, on notera
![\begin{theorem}[Dirichlet]
Soit $f\in L^1_p([-\pi,\pi])$. Soit $t_0$\ un point t...
... \to \frac1{2}\left(f(t_{0+}) + f(t_{0-}) \right)\ .
\end{equation}\end{theorem}](img109.png)
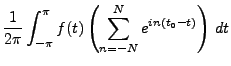
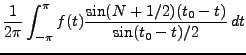
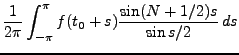
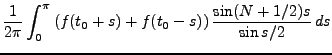
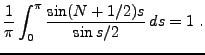
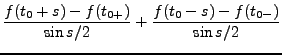
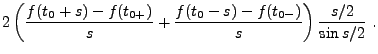
![[*]](crossref.png) ) pour conclure.
) pour conclure.
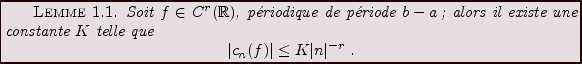
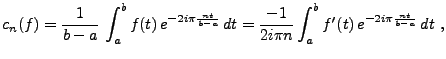
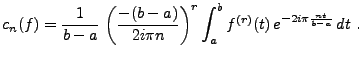
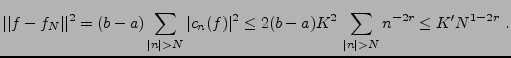
![]() , à support borné dans l'intervalle
, à support borné dans l'intervalle ![]() .
Soit
.
Soit ![]() la fonction périodique de période
la fonction périodique de période ![]() , qui coïncide
avec
, qui coïncide
avec ![]() sur
sur ![]() , définie par
, définie par
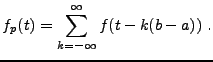
![$\displaystyle f_N(t) = \left(\sum_{n=-N}^N c_n(f) e^{2i\pi nt/(b-a)}\right)\, \chi_{[a,b]}(t)\ ,$](img155.png)
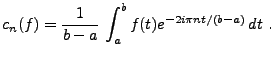
![]() est unique. Cependant, le
passage de
est unique. Cependant, le
passage de ![]() à
à ![]() n'est pas la seule possibilité. Il
existe de multiples alternatives, dont on va donner deux exemples ci dessous.
n'est pas la seule possibilité. Il
existe de multiples alternatives, dont on va donner deux exemples ci dessous.
![]() , définie sur l'intervalle
, définie sur l'intervalle
![]() par
par
![$\displaystyle g(t) =\left\{\begin{array}{ll}
f(t) &\hbox{ si }t\in [a,b]\\
f(2a-t) &\hbox{ si }t\in [2a-b,a]\ .
\end{array}\right.
$](img159.png)
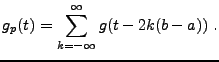
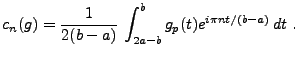
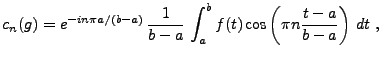
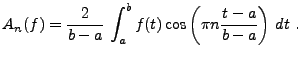
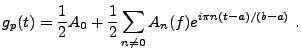
![$\displaystyle f_N^{(C)}(t) = \left(\frac1{2}A_0 +\sum_{n=1}^N A_n(f)\cos\left(\pi n\frac{t-a}{b-a}\right)\right)\chi_{[a,b]}(t)\ .$](img173.png)
![]() ) de
) de ![]() , mais une extension
antisymétrique
, mais une extension
antisymétrique ![]() , définie par
, définie par
![$\displaystyle h(t) =\left\{\begin{array}{ll}
f(t) &\hbox{ si }t\in [a,b]\\
-f(2a-t) &\hbox{ si }t\in [2a-b,a]\ .
\end{array}\right.
$](img175.png)
![$\displaystyle f_N^{(S)}(t) = \left(\sum_{n=1}^N B_n(f)\sin\left(\pi n\frac{t-a}{b-a}\right)\right)\chi_{[a,b]}(t)\ ,$](img178.png)
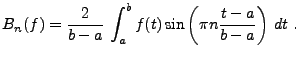
![]() .
Nous avons vu plus haut que celui-ci est directement lié à la
régularité, non pas de
.
Nous avons vu plus haut que celui-ci est directement lié à la
régularité, non pas de ![]() elle même, mais de la fonction
périodique utilisée dans le développement, c'est à dire
ici
elle même, mais de la fonction
périodique utilisée dans le développement, c'est à dire
ici ![]() , ou
, ou ![]() , ou la fonction équivalente dans le
cas du développement en série de sinus.
, ou la fonction équivalente dans le
cas du développement en série de sinus.
![]() est une fonction continue, il est rare qu'elle
soit telle que
est une fonction continue, il est rare qu'elle
soit telle que ![]() . Donc
. Donc ![]() est discontinue, et
les coefficients
est discontinue, et
les coefficients ![]() n'ont aucune raison de décroître
assez vite quand
n'ont aucune raison de décroître
assez vite quand ![]() est grand.
Par contre, si
est grand.
Par contre, si ![]() est continue, alors il est facile de voir que
est continue, alors il est facile de voir que
![]() est continue également, de sorte que les coefficients
est continue également, de sorte que les coefficients ![]() ont toutes les chances de décroître plus rapidement que
les coefficients
ont toutes les chances de décroître plus rapidement que
les coefficients ![]() .
.
![[*]](crossref.png) , avec l'approximation par
cosinus (qui est exacte, et identique à la série de Fourier
usuelle, et ne comporte qu'un terme) et l'approximation par une série
de sinus comportant 10 termes. La série de sinus convergera toujours
vers 0 en
, avec l'approximation par
cosinus (qui est exacte, et identique à la série de Fourier
usuelle, et ne comporte qu'un terme) et l'approximation par une série
de sinus comportant 10 termes. La série de sinus convergera toujours
vers 0 en 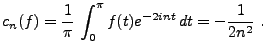
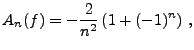
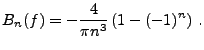
![[*]](crossref.png) et
et ![[*]](crossref.png) représentent les approximations obtenues
avec ces 3 développements, respectivement
représentent les approximations obtenues
avec ces 3 développements, respectivement ![[*]](crossref.png) représente
l'erreur d'approximation dans les 3 cas:
représente
l'erreur d'approximation dans les 3 cas: 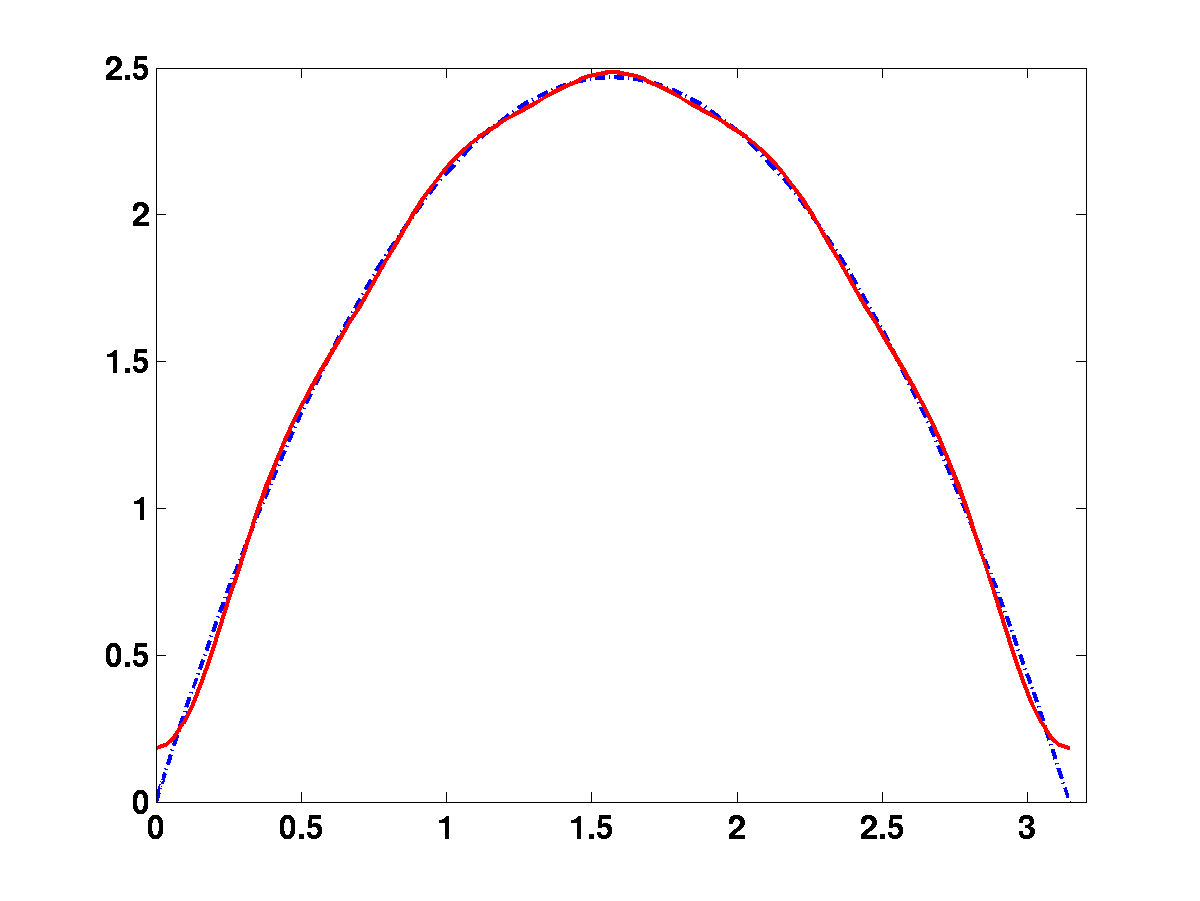
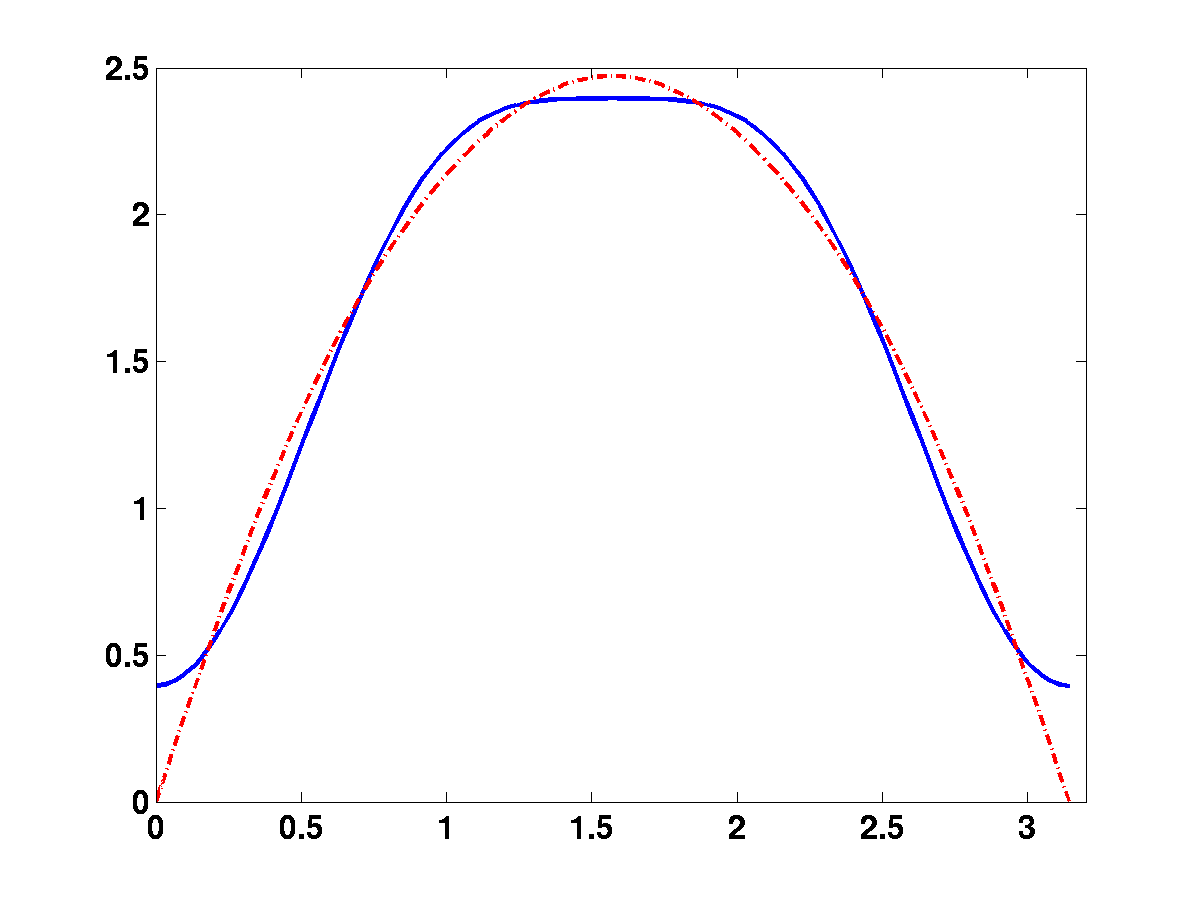
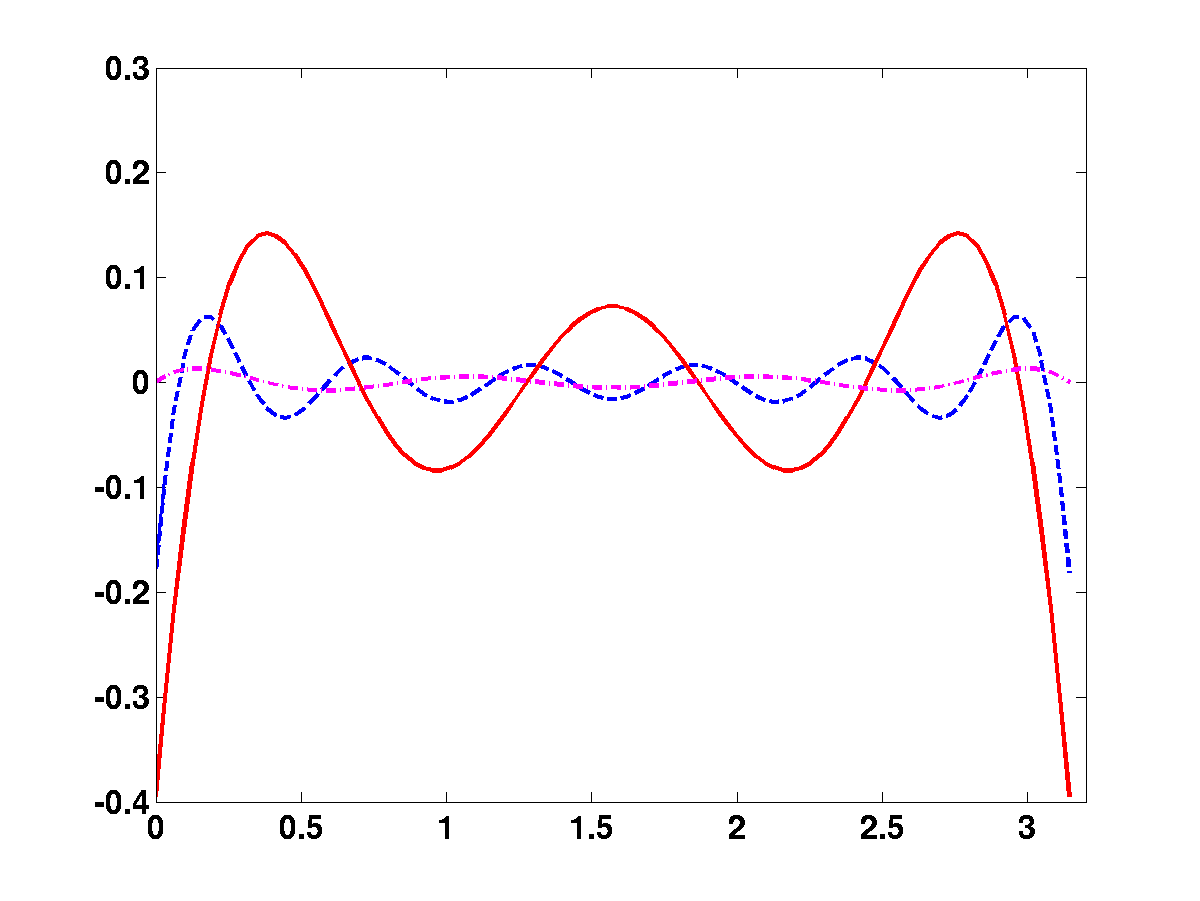
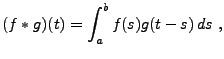
![\begin{proposition}[Young]
Soient $f\in L^p_p([a,b])$\ et $g\in L^q_p([a,b])$, o...
... \le C_{pq}\,\Vert f\Vert _p\,\Vert g\Vert _q\ .
\end{equation}\end{proposition}](img201.png)
![]() , et
, et
![]() ;
il résulte des inégalités d'Young que
;
il résulte des inégalités d'Young que
![]() .
On peut donc calculer
.
On peut donc calculer
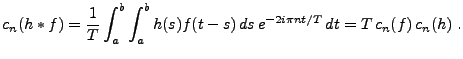
![]() . Alors, d'après
l'inégalité de Cauchy-Schwarz,
. Alors, d'après
l'inégalité de Cauchy-Schwarz,
![]() , et on
peut calculer les coefficients de Fourier
, et on
peut calculer les coefficients de Fourier
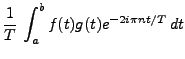
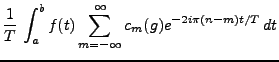
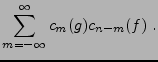
![\begin{proposition}
Soient $f,g\in L^2_p([a,b])$. Les coefficients de Fourier $c...
...n-m}(g)\\
c_n(f*g) &=& (b-a)\,c_n(f)\,c_n(g)\ .
\end{eqnarray}\end{proposition}](img214.png)
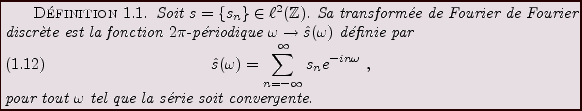

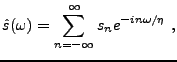


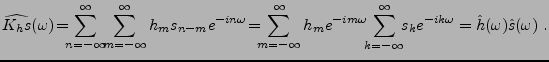
![]() , il est facile de voir que l'opérateur
linéaire
, il est facile de voir que l'opérateur
linéaire
![]() défini par
défini par
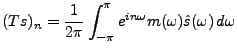
![]() . Un tel filtre est défini par sa fonction
de transfert
. Un tel filtre est défini par sa fonction
de transfert
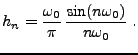
![[*]](crossref.png) : un signal (transitoire), et
deux versions filtrées avec des fréquences de coupure différentes.
On voit bien l'effet du filtrage qui atténue fortement les composantes
les plus rapidement variables dans le signal. En particulier, dans le premier
signal filtré (figure du milieu), les composantes très rapidement
variables (donc les très hautes fréquences) ont été supprimées,
mais des oscillations régulières subsistent. Par contre, dans le second
exemple (figure du bas) obtenu avec une fréquence de coupure
: un signal (transitoire), et
deux versions filtrées avec des fréquences de coupure différentes.
On voit bien l'effet du filtrage qui atténue fortement les composantes
les plus rapidement variables dans le signal. En particulier, dans le premier
signal filtré (figure du milieu), les composantes très rapidement
variables (donc les très hautes fréquences) ont été supprimées,
mais des oscillations régulières subsistent. Par contre, dans le second
exemple (figure du bas) obtenu avec une fréquence de coupure
![]() inférieure à la précédente, ces oscillations ont
été supprimées.
inférieure à la précédente, ces oscillations ont
été supprimées.
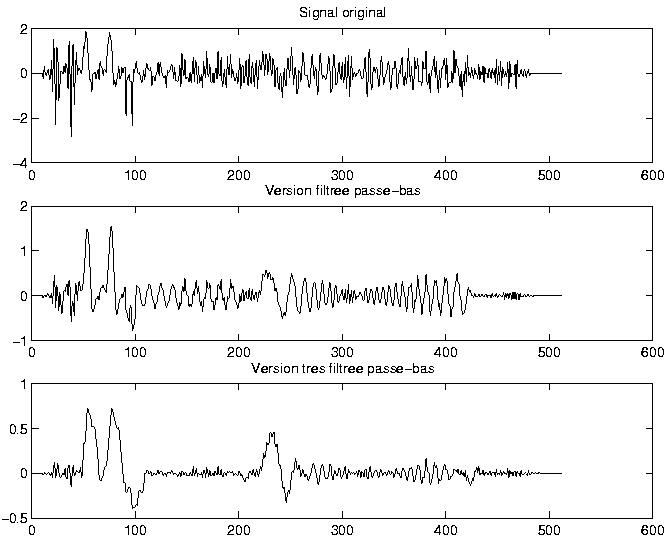
![]() soit de support fini:
soit de support fini:
![]() seulement si
seulement si
![]() . La fonction
de transfert est alors un polynôme trigonométrique
. La fonction
de transfert est alors un polynôme trigonométrique
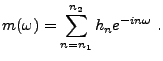
![]() la suite
la suite ![]() définie par
définie par
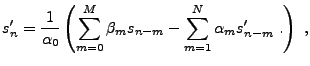
![]() , ou tout du moins un filtre stable. Pour cela, remarquons que
les signaux d'entrée
, ou tout du moins un filtre stable. Pour cela, remarquons que
les signaux d'entrée ![]() et de sortie
et de sortie ![]() du
filtre sont reliés par une relation du type
du
filtre sont reliés par une relation du type

![]() du filtre correspondant est une
fonction périodique, et peut être décomposée en
série de Fourier. Cependant, celle-ci est (sauf dans certains
cas triviaux) une série infinie, de sorte que le filtre
considéré est bel et bien un filtre IIR.
L'expression (
du filtre correspondant est une
fonction périodique, et peut être décomposée en
série de Fourier. Cependant, celle-ci est (sauf dans certains
cas triviaux) une série infinie, de sorte que le filtre
considéré est bel et bien un filtre IIR.
L'expression (![[*]](crossref.png) ) montre donc qu'il est possible d'effectuer
un filtrage IIR en n'utilisant qu'un nombre fini d'opérations. Cette
remarque est d'une importance considérable en pratique.
) montre donc qu'il est possible d'effectuer
un filtrage IIR en n'utilisant qu'un nombre fini d'opérations. Cette
remarque est d'une importance considérable en pratique.
![]() , et
en particulier des zéros de son dénominateur. Ce dernier étant
(tout comme le numérateur) un polynôme trigonométrique,
c'est donc un polynôme dans la variable complexe
, et
en particulier des zéros de son dénominateur. Ce dernier étant
(tout comme le numérateur) un polynôme trigonométrique,
c'est donc un polynôme dans la variable complexe
![]() ,
ce qui rend l'étude des zéros plus facile. Les zéros du
numérateur et du dénominateur sont les racines de polynômes
en
,
ce qui rend l'étude des zéros plus facile. Les zéros du
numérateur et du dénominateur sont les racines de polynômes
en ![]() correspondants, ces dernières étant en général
complexes. Ceci suggère d'utiliser des techniques de fonctions
d'une variable complexe, et conduit naturellement à introduire
un outil voisin de la TFD, à savoir la transformation en
correspondants, ces dernières étant en général
complexes. Ceci suggère d'utiliser des techniques de fonctions
d'une variable complexe, et conduit naturellement à introduire
un outil voisin de la TFD, à savoir la transformation en ![]() .
.
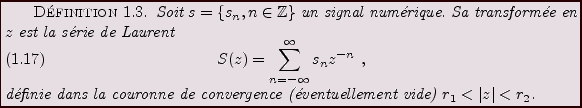
![]() est holomorphe dans sa couronne de convergence.
Inversement, étant donnée une fonction
est holomorphe dans sa couronne de convergence.
Inversement, étant donnée une fonction ![]() holomorphe dans une
couronne
holomorphe dans une
couronne
![]() , elle admet un unique développement
en série de Laurent.
De plus, on a le lemme
classique suivant:
, elle admet un unique développement
en série de Laurent.
De plus, on a le lemme
classique suivant:

![]() d'un signal numérique:
d'un signal numérique:

![]() est anticausal,
est anticausal, ![]() , et
, et ![]() est bien défini
à l'intérieur du cercle de rayon
est bien défini
à l'intérieur du cercle de rayon ![]() .
.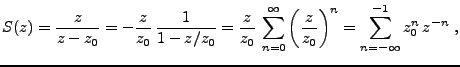
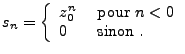
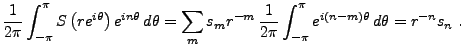
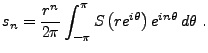
![\begin{proposition}
Soit $s$\ un signal num\'erique, et soit $S$\ sa transform\'...
...\'e sur l'origine du plan complexe,
de rayon $r\in ]r_1,r_2[$.
\end{proposition}](img294.png)
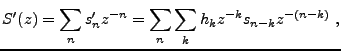
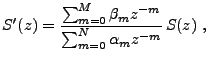
![[*]](crossref.png) ) obtenue avec la TFD.
) obtenue avec la TFD.
![[*]](crossref.png) ).
On impose que le filtre
).
On impose que le filtre ![]() et
et ![]() sont réels.
Dans ce cas, il est facile de voir que
sont réels.
Dans ce cas, il est facile de voir que
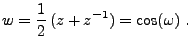
![]() une fonction rationnelle positive. Notons
une fonction rationnelle positive. Notons
![]() , et
, et ![]() les zéros (dans le plan complexe) de
les zéros (dans le plan complexe) de ![]() (le numérateur
(le numérateur ![]() se traite de façon identique). On voit facilement que l'équation
en
se traite de façon identique). On voit facilement que l'équation
en ![]()
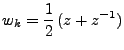
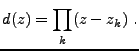
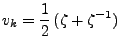
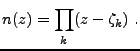


![[*]](crossref.png)
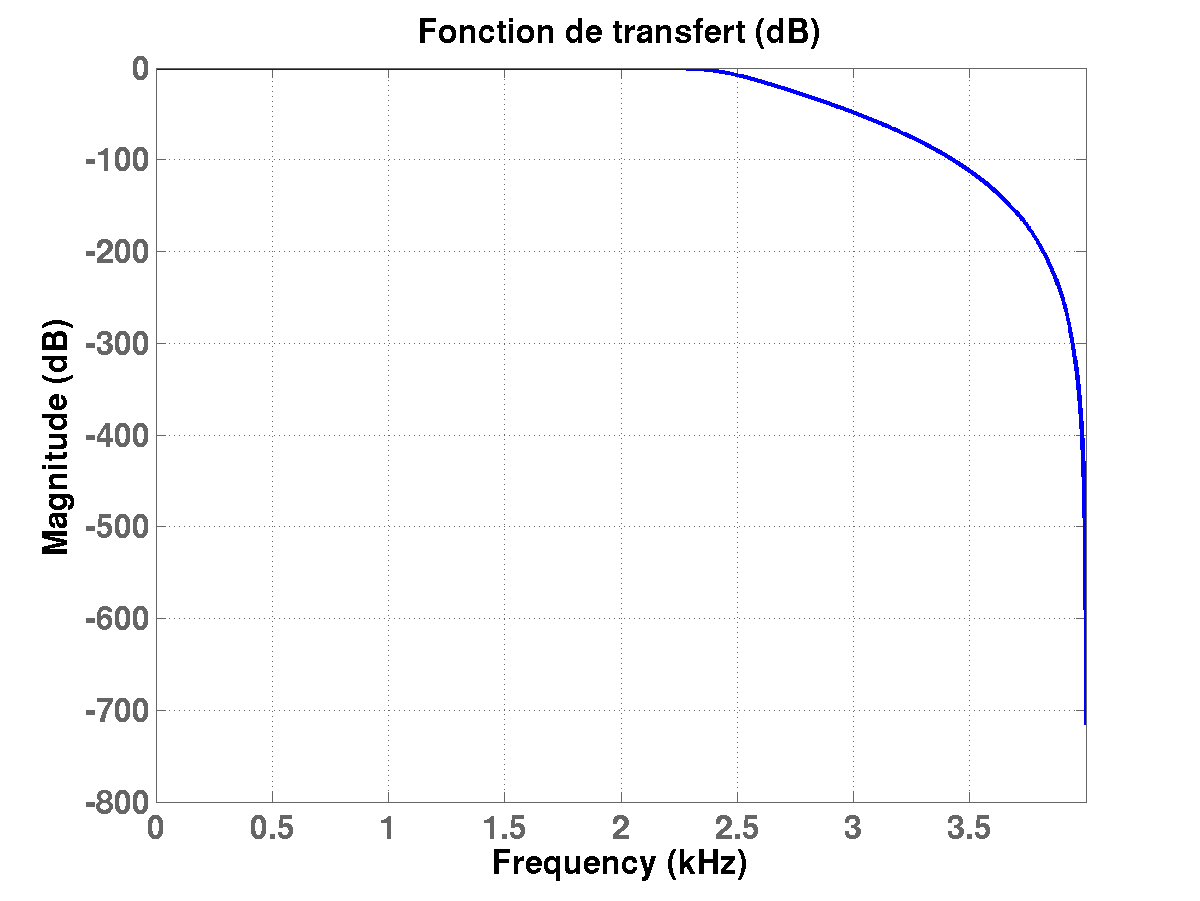
![[*]](crossref.png) . Par
conséquent, il est toujours possible de trouver un filtre causal
d'ordre fini, de réponse impulsionnelle
. Par
conséquent, il est toujours possible de trouver un filtre causal
d'ordre fini, de réponse impulsionnelle ![[*]](crossref.png) ) soit satisfaite.
) soit satisfaite.
![]() contrôle en fait la fréquence de coupure, via la relation
contrôle en fait la fréquence de coupure, via la relation
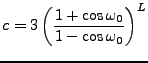
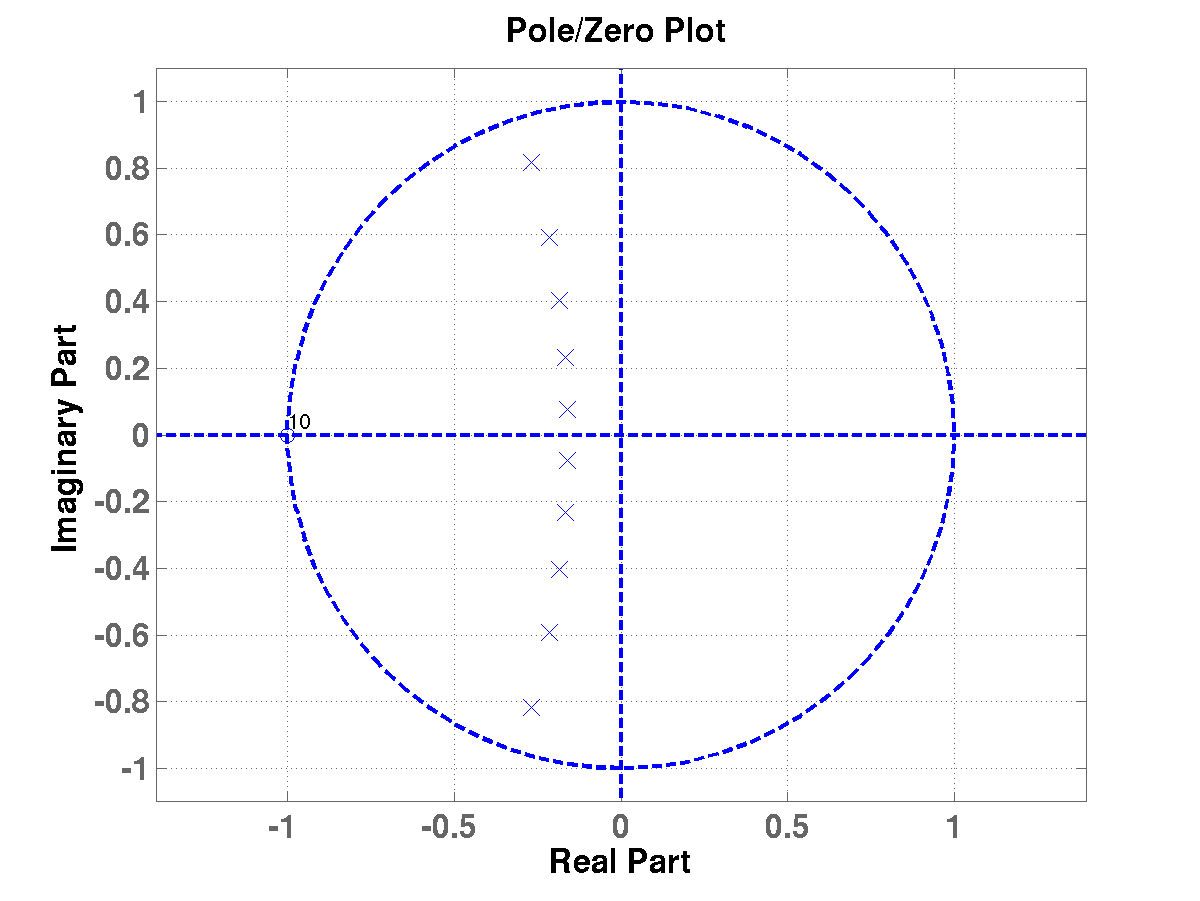
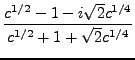
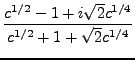
![[*]](crossref.png) les positions des pôles, c'est à dire des racines du
dénominateur (croix) et des zéros (cercles) de
les positions des pôles, c'est à dire des racines du
dénominateur (croix) et des zéros (cercles) de 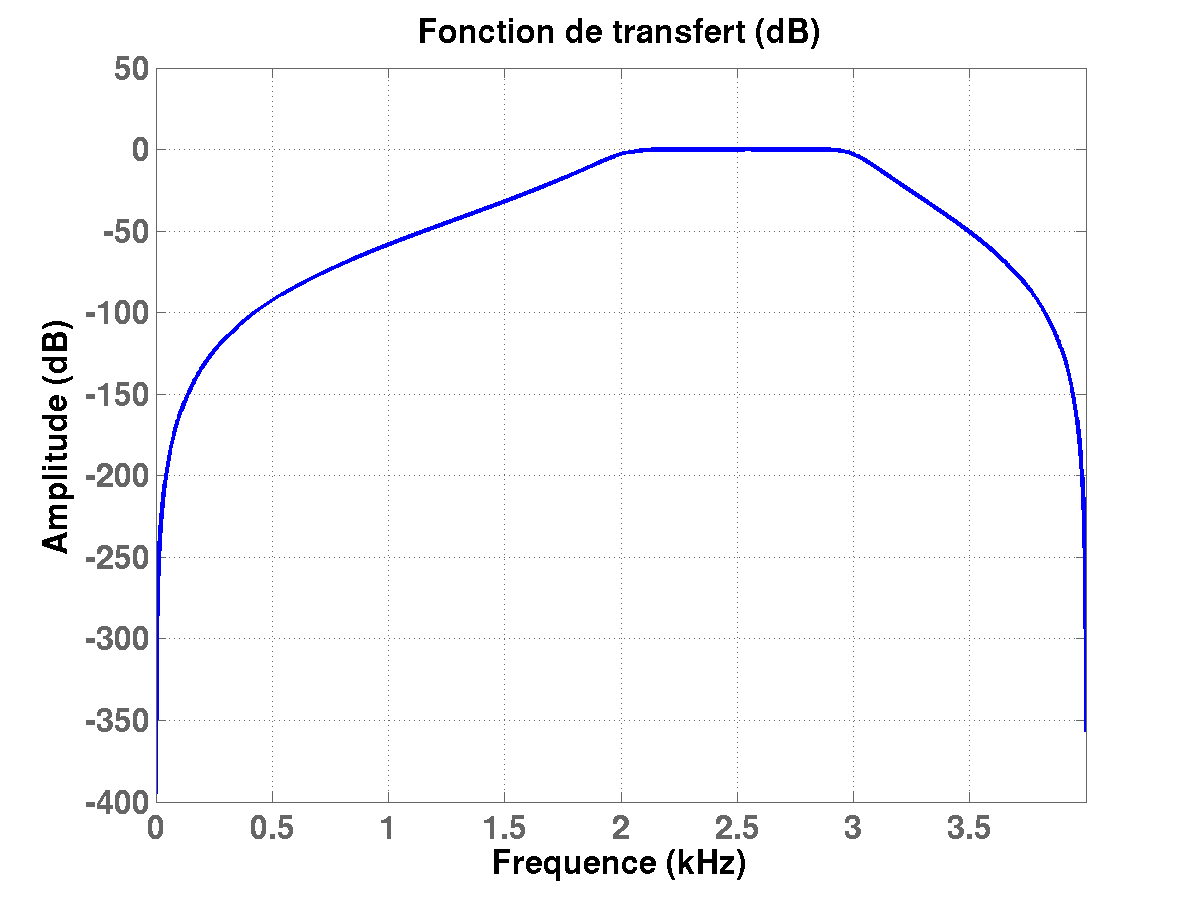
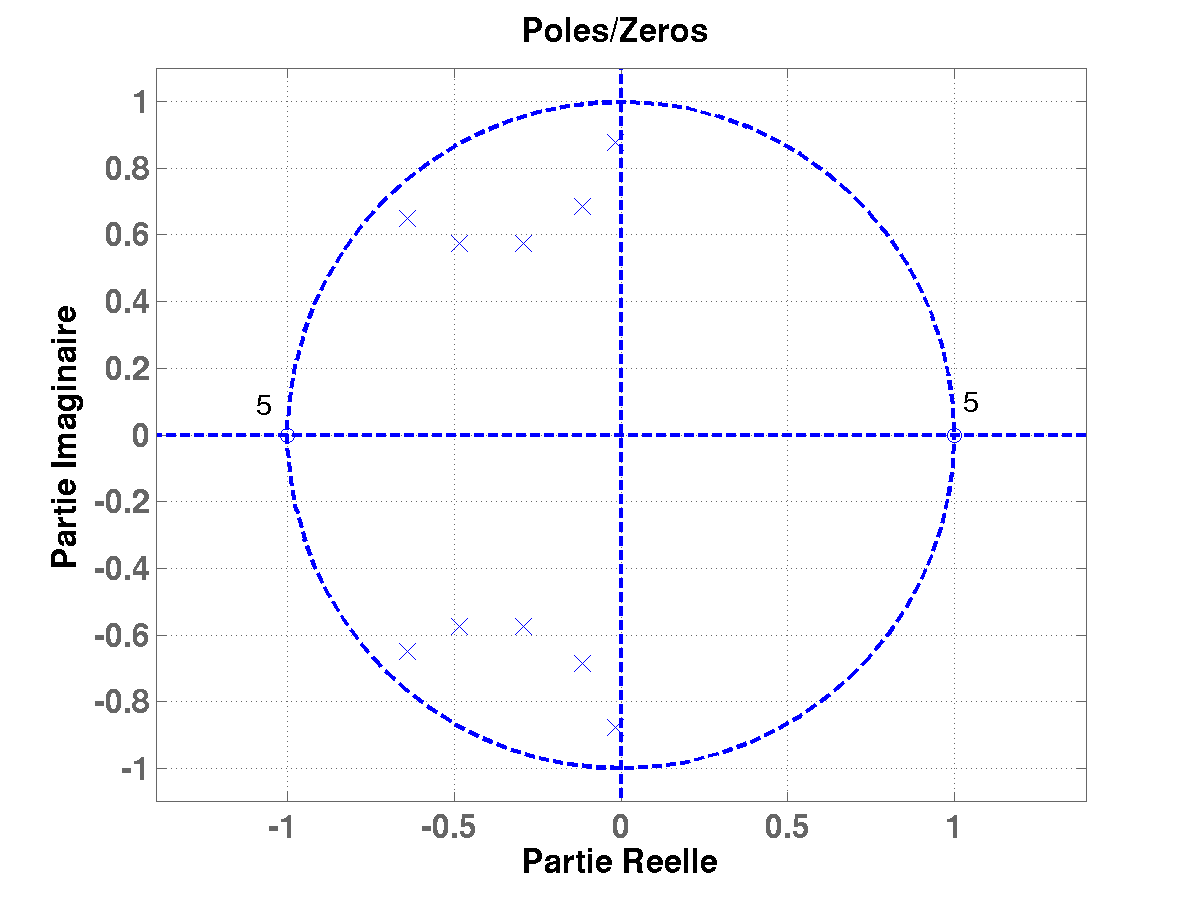
![]() , notées
, notées
![]() ,
,
![]() , qui sont donc
de la forme
, qui sont donc
de la forme
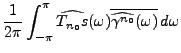
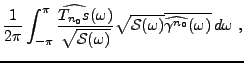
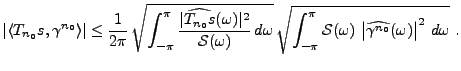
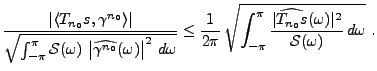
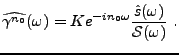
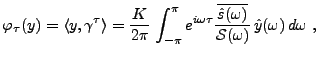
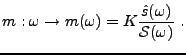
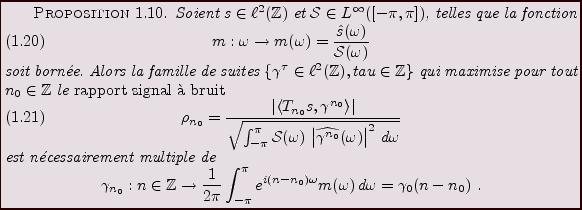
![]() correspondante prend la
forme d'un filtre numérique, de fonction de transfert
correspondante prend la
forme d'un filtre numérique, de fonction de transfert ![]() :
:
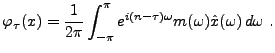
![[*]](crossref.png) ) avec un
) avec un ![[*]](crossref.png) . Comme on le voit, le signal de
sortie du filtre adapté présente un ``pic'', c'est à dire
un maximum bien marqué à la position où le signal de départ
décalé était présent.
. Comme on le voit, le signal de
sortie du filtre adapté présente un ``pic'', c'est à dire
un maximum bien marqué à la position où le signal de départ
décalé était présent.
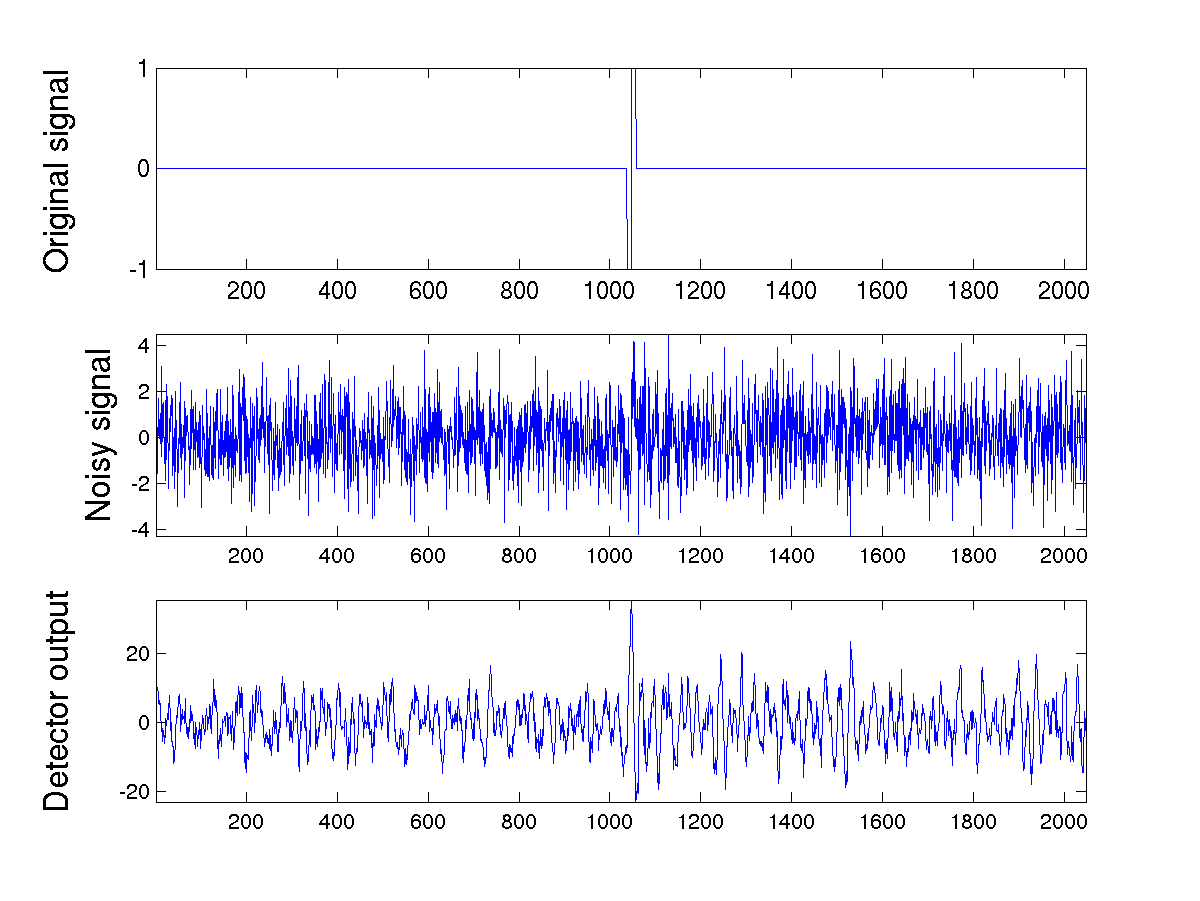
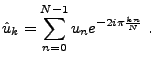
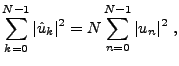
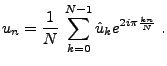
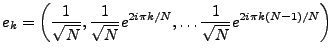

![]() à partir des
à partir des ![]() et de la somme de la
série géométrique.
et de la somme de la
série géométrique.
![]()
![]() n'est pas à support
fini, il est néanmoins facile d'obtenir une estimation de sa
transformée de Fourier à partir d'un ``segment'' fini, et des
estimations d'erreur grâce à la formule de Parseval.
n'est pas à support
fini, il est néanmoins facile d'obtenir une estimation de sa
transformée de Fourier à partir d'un ``segment'' fini, et des
estimations d'erreur grâce à la formule de Parseval.
![]() -dimensionnel est défini comme
une suite à
-dimensionnel est défini comme
une suite à ![]() indices
indices
![[*]](crossref.png) . L'axe horizontal est l'axe
. L'axe horizontal est l'axe ![]() , et l'axe
vertical est l'axe
, et l'axe
vertical est l'axe ![]() . Un point
. Un point ![]() est appelé
pixel. La valeur de l'image
est appelé
pixel. La valeur de l'image
![]() au pixel
au pixel
![]() est représentée par un niveau de gris d'intensité
proportionnelle à
est représentée par un niveau de gris d'intensité
proportionnelle à
![]() .
.
![]() , c'est à dire celui des signaux
dits d'énergie finie, tels que
, c'est à dire celui des signaux
dits d'énergie finie, tels que
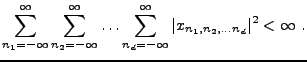


![]() dans la direction 1, et
dans la direction 1, et ![]() dans
la direction 2. Comme dans le cas 1D, plus la fréquence est élevée,
plus les oscillations sont rapides.
dans
la direction 2. Comme dans le cas 1D, plus la fréquence est élevée,
plus les oscillations sont rapides.![]() indices
indices ![]() , le filtre linéaire
, le filtre linéaire
![]() de réponse impulsionnelle
de réponse impulsionnelle ![]() est l'opérateur linéaire
qui associe à tout signal numérique
est l'opérateur linéaire
qui associe à tout signal numérique ![]() -dimensionnel
-dimensionnel ![]() le signal
le signal ![]() défini par
défini par
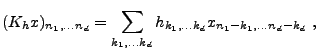
![]() , on montre facilement que
, on montre facilement que
![$\displaystyle (K_h x)_{n_1,\dots n_d} = \frac1{(2\pi)^d}\int_{[-\pi,\pi]^d} m(\...
...at x(\xi_1,\dots,\xi_d) e^{i(n_1\xi_1 +\dots +n_d\xi_d)}\,d\xi_1\dots d\xi_d\ .$](img413.png)
![[*]](crossref.png) .
.
![$\displaystyle m(\xi_1,\xi_2) = \chi_{[0,\omega_0]}(\sqrt{\xi_1^2 + \xi_2^2})\ .
$](img415.png)
![[*]](crossref.png) .
On se focalise ici sur les bases orthonormales,
et on donne quelques exemples de bases ``classiques''.
.
On se focalise ici sur les bases orthonormales,
et on donne quelques exemples de bases ``classiques''.
![[*]](crossref.png) que les sinusoïdes
que les sinusoïdes
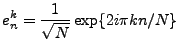
![]() appelées bases
DCT (pour Discrete Cosine Transform). Ces dernières
existent en huit versions différentes, les deux plus ``populaires''
étant:
appelées bases
DCT (pour Discrete Cosine Transform). Ces dernières
existent en huit versions différentes, les deux plus ``populaires''
étant:
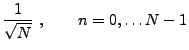
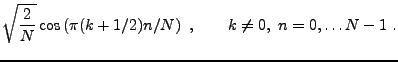
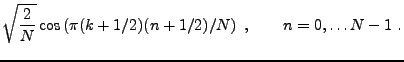
![]() , où
, où ![]() est un entier positif fixé.
Le découpage consiste à écrire
est un entier positif fixé.
Le découpage consiste à écrire
![]() sous la forme de somme
directe
sous la forme de somme
directe
![]() une base orthonormale
de
une base orthonormale
de
![]() . Pour tout
. Pour tout
![]() , soit
, soit ![]() la copie du vecteur
la copie du vecteur
![]() définie par décalage de
définie par décalage de ![]() :
:
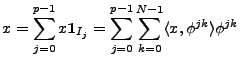
![[*]](crossref.png) . En quelques mots, les repères
constituent une généralisation de la notion de famille génératrice
de vecteurs, adaptable aux espaces de Hilbert de dimension infinie. Un
repère dans un espace de Hilbert
. En quelques mots, les repères
constituent une généralisation de la notion de famille génératrice
de vecteurs, adaptable aux espaces de Hilbert de dimension infinie. Un
repère dans un espace de Hilbert
![]() est une famille de vecteurs
est une famille de vecteurs
![]() telle qu'il existe deux
constantes strictement positives
telle qu'il existe deux
constantes strictement positives
![]() vérifiant,
pour tout
vérifiant,
pour tout
![]() ,
,
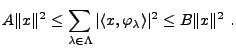
![[*]](crossref.png) ) que dans ces conditions,
l'opérateur d'analyse
) que dans ces conditions,
l'opérateur d'analyse
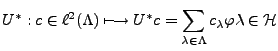
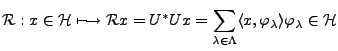
![]() , on a une formule
de type ``formule de Parseval''
, on a une formule
de type ``formule de Parseval''
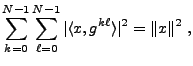
![]() sous la forme
sous la forme