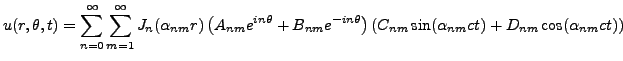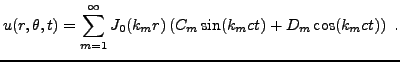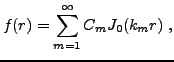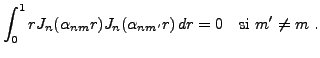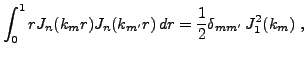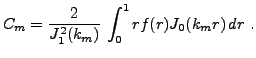Subsections
Terminons ce chapitre par une rapide discussion des problèmes
hyperboliques, qui décrivent les phénomènes de propagation
d'ondes par exemple.
L'exemple le plus simple et classique est celui de l'équation
aux dérivées partielles décrivant les vibrations transversales
d'une corde de violon (ou piano); si on note 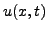 la position du
point
la position du
point 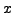 de la corde à l'instant
de la corde à l'instant 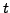 , on a
, on a
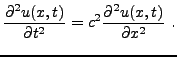 |
(3.32) |
Comme on l'a vu plus haut, cette équation signifie qu'à
tout instant 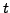 s'exerce au point
s'exerce au point 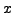 une force de rappel
proportionnelle à la concavité
une force de rappel
proportionnelle à la concavité
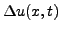 de
de 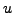 en
en 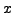 .
.
Bien qu'il ne s'agisse pas d'une équation du second ordre,
l'équation régissant les vibrations d'une poutre
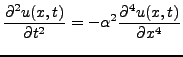 |
(3.33) |
conduit à des solutions possédant des propriétés qualitatives
similaires.
Commençons par le cas unidimensionnel en espace.
L'équation des ondes (![[*]](crossref.png) ) possède des solutions
simples. Il s'avère avantageux dans ce cas d'introduire les
variables
) possède des solutions
simples. Il s'avère avantageux dans ce cas d'introduire les
variables
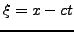 et
et
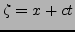 . On a alors
. On a alors
et
de sorte que (![[*]](crossref.png) ) est équivalente
à l'équation
) est équivalente
à l'équation
En intégrant une première fois par rapport à 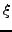 , on obtient
, on obtient
une fonction ne dépendant que de 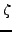 . En intégrant cette fois
par rapport à
. En intégrant cette fois
par rapport à 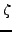 , on obtient finalement
, on obtient finalement
d'où la solution de d'Alembert
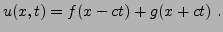 |
(3.34) |
On obtient ainsi deux ondes  et
et 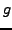 , se propageant respectivement
dans la direction des
, se propageant respectivement
dans la direction des 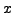 positifs (onde progressive) et négatifs
(onde régressive). Les fonctions
positifs (onde progressive) et négatifs
(onde régressive). Les fonctions  et
et 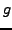 sont déterminées à partir des conditions initiales
sont déterminées à partir des conditions initiales
qui conduit au système
qui peut ensuite être résolu directement.
Le cas tridimensionnel est plus complexe, commençons par la
remarque suivante.
On considère l'équation des ondes dans l'espace
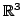
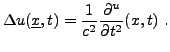 |
(3.35) |
Cherchons des solutions particulières de la forme
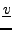 étant un vecteur fixé. On voit facilement que
étant un vecteur fixé. On voit facilement que
de sorte qu'un tel
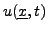 est bien solution, à condition que
est bien solution, à condition que
Ainsi, la condition obtenue porte uniquement sur la norme du vecteur
vitesse, et pas sur sa direction. Ceci laisse beaucoup de liberté,
et conduit aux ondes sphériques, comme on va le voir.
Considérons le problème défini par l'équation des
ondes (![[*]](crossref.png) ) dans l'espace
) dans l'espace
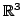 , complété par les
conditions initiales
, complété par les
conditions initiales
pour un couple de fonctions  donné.
donné.

On se place dans le cas unidimensionnel, et on s'intéresse à
l'équation
![$\displaystyle \frac{\partial^2}{\partial t^2} u(x,t) = c^2\frac{\partial^2}{\partial x^2} u(x,t)\ ,\quad t\in{\mathbb{R}}^+,\ x\in[0,L]\ .$](img806.png) |
(3.38) |
La solution de cette équation peut être utilisée pour décrire
un grand nombre de situations physiques différentes, comme par exemple
- des ondes acoustiques (transverses),
- des vibrations dans les solides (longitudinales, transverses ou
ondes de torsion),
- des ondes de probabilité en mécanique quantique,
- les vibrations (transverses) d'une corde
- ...
C'est ce dernier exemple qu'on prendra comme illustration.
On considère généralement trois types de conditions au bord.
- Une condition de type Dirichlet, qu'on appelle dans ce cas
condition de bords contrôlés
- Une condition de type Neumann, qui revient à exercer
sur les bords des forces fixées
- Une condition mixte, qui revient à supposer
un lien élastique sur les bords
La méthode de résolution suit fidèlement celle employée
pour l'équation de la chaleur. On recherche des solutions sous forme de
fonctions à variables séparées
ce qui conduit à deux équations pour les deux fonctions
Suivant les valeurs de 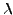 , on sera confronté à divers
types de solutions. Dans la mesure où
, on sera confronté à divers
types de solutions. Dans la mesure où 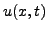 représente la position
d'un point d'une corde, il est naturel de se limiter à des valeurs
réelles de
représente la position
d'un point d'une corde, il est naturel de se limiter à des valeurs
réelles de 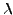 . On a donc les trois situations
. On a donc les trois situations
- Si
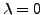 , les solutions sont de la forme
, les solutions sont de la forme
La solution ne sera bornée que si  , et ne satisfera les
conditions au bord que si
, et ne satisfera les
conditions au bord que si 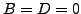 . Reste donc la seule solution nulle
. Reste donc la seule solution nulle
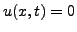 .
.
- Si
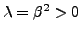 , les solutions sont de la forme
, les solutions sont de la forme
et là encore, seule la solution nulle est admissible.
- Si
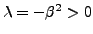 , les solutions sont de la forme
, les solutions sont de la forme
Seul le dernier cas de figure convient. En imposant les conditions
aux bords, on voit facilement que 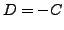 ,d e sorte que la solution
prend la forme
,d e sorte que la solution
prend la forme
avec
La solution générale est donc de la forme
 |
(3.41) |
Pour conclure, il faut maintenant imposer les conditions initiales, que
l'on prend de la forme
On aboutit alors au système
d'où on déduit, grâce au lemme ![[*]](crossref.png) , le système
, le système
et de là
On se propose ici d'étudier les vibrations d'une membrane de tambour,
décrites par une équation des ondes bidimensionnelle. On
suppose que le bord de la membrane est un cercle de rayon 1, et
on note
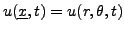 la hauteur du point de
coordonnées polaires
la hauteur du point de
coordonnées polaires
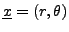 de la membrane à l'instant
de la membrane à l'instant
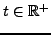 . En écrivant le Laplacien en coordonnées polaires,
l'évolution de
. En écrivant le Laplacien en coordonnées polaires,
l'évolution de 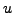 est décrite par l'équation des ondes
est décrite par l'équation des ondes
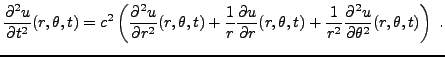 |
(3.42) |
Cette équation est complétée par la condition au bord
ainsi que les conditions initiales
On recherche des solutions à variables séparées
ce qui conduit au système
où 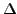 est le Laplacien spatial, exprimé en coordonnées polaires.
est le Laplacien spatial, exprimé en coordonnées polaires.
L'équation temporelle est facile à résoudre, et conduit à des
solutions de la forme
Considérons maintenant l'équation
d'Helmholtz (![[*]](crossref.png) ), complétée par la condition
au bord
), complétée par la condition
au bord
On recherche encore une fois des solutions sous forme de fonction à
variables séparées
ce qui conduit aux deux équations
où on a pris la constante de séparation égale à 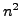 .
.
Il s'agit d'un problème que nous avons déjà rencontré au
chapitre ![[*]](crossref.png) .
Encore une fois, l'équation angulaire est facile à résoudre,
et conduit à des solutions
.
Encore une fois, l'équation angulaire est facile à résoudre,
et conduit à des solutions
qui impose
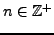 De plus on sait que la solution de l'équation radiale est donnée
par les fonctions de Bessel de première espèce
et deuxième espèce
De plus on sait que la solution de l'équation radiale est donnée
par les fonctions de Bessel de première espèce
et deuxième espèce
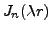 et
et
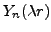 .
Ces dernières étant non bornées, on a donc des solutions de la forme
.
Ces dernières étant non bornées, on a donc des solutions de la forme
On doit maintenant imposer la condition au bord
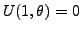 . Ceci
impose
. Ceci
impose
c'est à dire que la constante de séparation 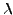 doit être
un zéro
doit être
un zéro
 de la fonction de Bessel
de la fonction de Bessel 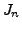 . Par conséquent
. Par conséquent
Ainsi, la solution générale de notre problème est de la forme
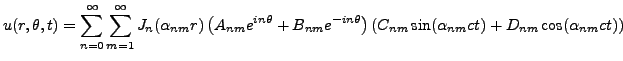 |
(3.47) |
La dernière étape consiste à calculer les constantes
à partir des conditions initiales. Le cas général est assez
difficile à traiter, on se limitera ici au cas particulier où
la condition initiale dépend uniquement de la variable radiale
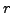 . En d'autres termes, on considère le cas
. En d'autres termes, on considère le cas
Dans ce cas, il est possible de montrer que seuls sont
présents les termes faisant intervenir la fonction de Bessel
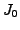 , et on a, en posant
, et on a, en posant
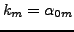
La condition
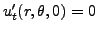 impose
impose 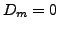 , et il reste donc à
déterminer les constantes
, et il reste donc à
déterminer les constantes 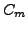 . On écrit pour cela
. On écrit pour cela
et on utilise maintenant un résultat obtenu au chapitre
précédent, à savoir l'orthogonalité
des fonctions de Bessel
Dans notre cas, on obtient, après calcul
d'où on déduit les constantes cherchées
Bruno Torresani
2007-06-26
![[*]](crossref.png) ) possède des solutions
simples. Il s'avère avantageux dans ce cas d'introduire les
variables
) possède des solutions
simples. Il s'avère avantageux dans ce cas d'introduire les
variables
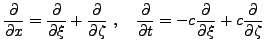
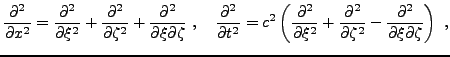
![[*]](crossref.png) ) est équivalente
à l'équation
) est équivalente
à l'équation
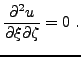
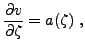
![]() et
et ![]() , se propageant respectivement
dans la direction des
, se propageant respectivement
dans la direction des ![]() positifs (onde progressive) et négatifs
(onde régressive). Les fonctions
positifs (onde progressive) et négatifs
(onde régressive). Les fonctions ![]() et
et ![]() sont déterminées à partir des conditions initiales
sont déterminées à partir des conditions initiales
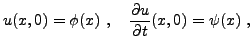
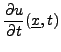
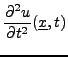
![[*]](crossref.png) ) dans l'espace
) dans l'espace
![]() , complété par les
conditions initiales
, complété par les
conditions initiales


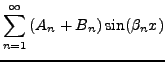
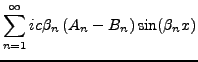
![[*]](crossref.png) , le système
, le système
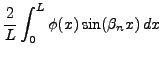
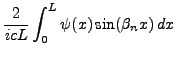
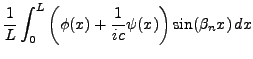
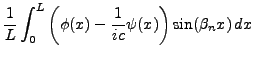
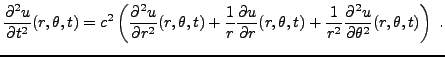
![[*]](crossref.png) ), complétée par la condition
au bord
), complétée par la condition
au bord
![[*]](crossref.png) .
Encore une fois, l'équation angulaire est facile à résoudre,
et conduit à des solutions
.
Encore une fois, l'équation angulaire est facile à résoudre,
et conduit à des solutions